Упр.834 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)

Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 8 класс, Просвещение:
834. При пересечении биссектрис всех углов прямоугольника образовался четырёхугольник. Докажите, что этот четырёхугольник — квадрат.
Дано:
ABCD-прямоуг;
AE,BE-биссект;
CG,DG-биссект;
Доказать:
EFGH-квадр;
Решение:
1) В прямоугольнике ABCD:
угол A=угол B=угол C=угол D=90°;
AB=CD, BC=AD;
2) Рассмотрим треугольник BEA:
угол BAE=угол ABE=1/2•90°=45°;
угол E=180°-(угол A+угол B)=90°;
3) Рассмотрим треугольник CGD:
угол DCG=угол CDG=1/2•90°=45°;
угол G=180°-(угол C+угол D)=90°;
4) Рассмотрим треугольник AFD:
угол DAF=угол ADF=1/2•90°=45°;
угол F=180°-(угол A+угол D)=90°;
угол A=угол D, AF=DF;
5) По гипотенузе и углу:
AB=CD, угол BAE=угол CDG=45°;
треугольник ABE=треугольник CGD,отсюда DG=AE;
6) В четырехугольнике EFGH:
EF=AF-AE=DF-DG=FG;
угол FEH=угол BEA, угол FGH=угол CGD;
угол FEH=угол EFG=угол FGH=90°;
Что и требовалось доказать.
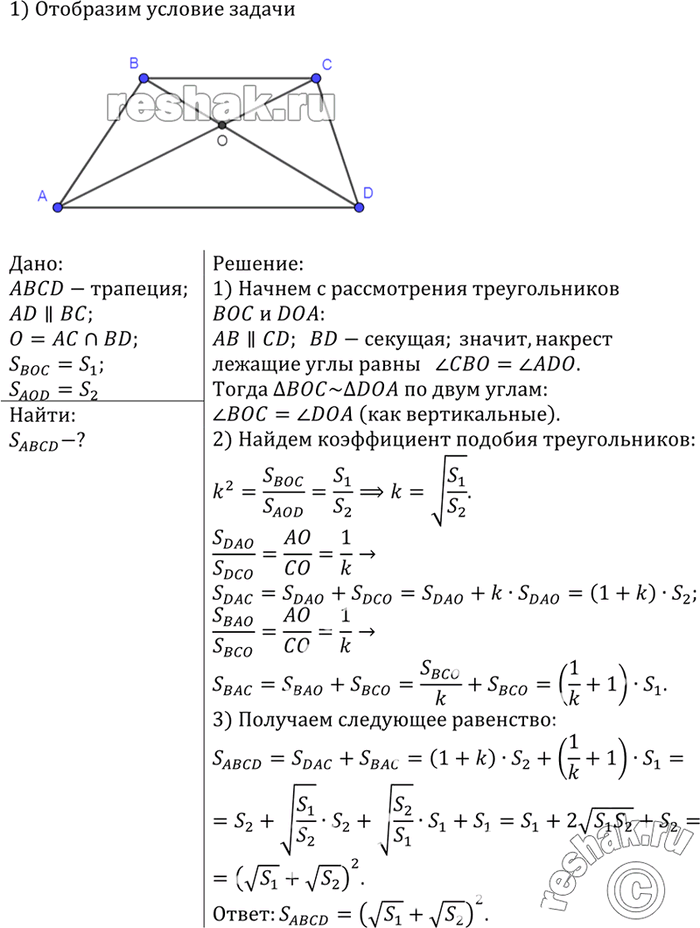
Диагонали трапеции ABCD с основаниями ВС и AD пересекаются в точке О. Площади треугольников БОС и AOD равны S1 и S2. Найдите площадь трапеции.
Похожие решебники
Популярные решебники 8 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.