Упр.669 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)

Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 8 класс, Просвещение:
669. Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведённую к основанию, в отношении 12:5, считая от вершины, а боковая сторона равна 60 см.
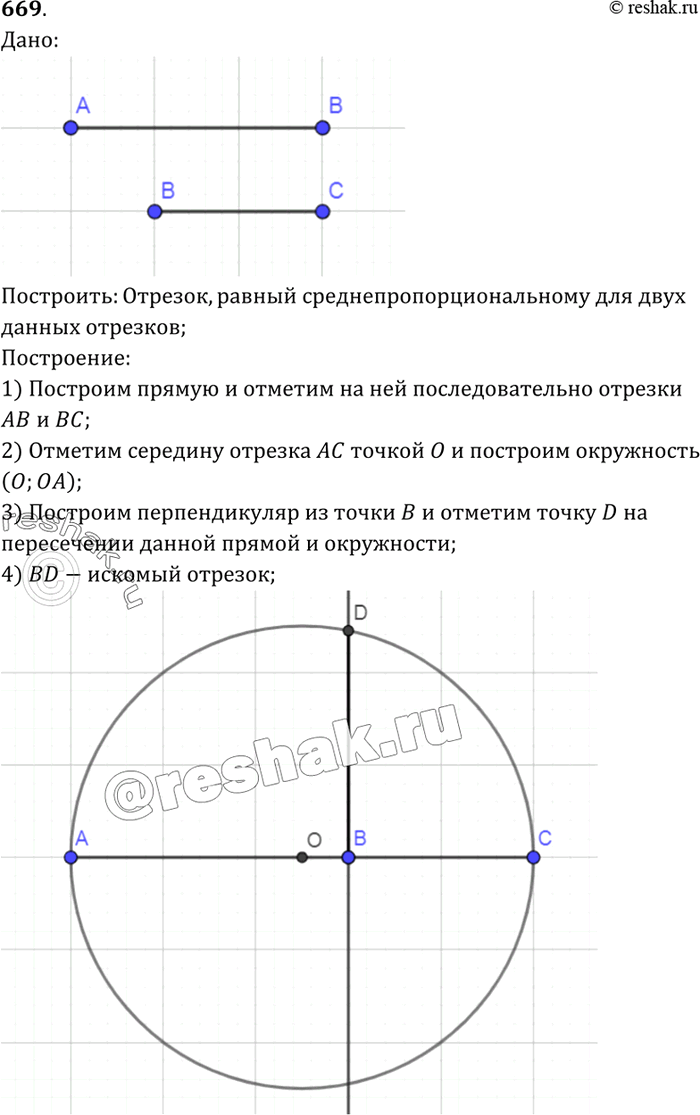
Дано:
O-ц.вп.окр;
BO:OH=12:5;
AB=BC=60 см;
Найти:
AC-?;
Решение:
1) Рассмотрим треугольник AHB и треугольник OEB:
угол B-общий; угол H=угол E=90°;
По первому признаку:
треугольник AHB=треугольник OEB, OE/AH=BE/BH=BO/AB;
2) В равнобедренном треугольник ABC:
OE=OH=r, BO=12/5 OH=12/5 r;
AH=(OE•AB)/BO=r•60•5/(12•r)=25;
AH=1/2•AC, AC=2•AH=50;
Ответ: 50 см.
Пользуясь утверждением, сформулированным в задаче 668, постройте отрезок, равный среднему пропорциональному для двух данных отрезков.
Похожие решебники
Популярные решебники 8 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







