Упр.407 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника
Атанасян, Бутузов 7 класс, Просвещение:
Задание учебника 2025 года
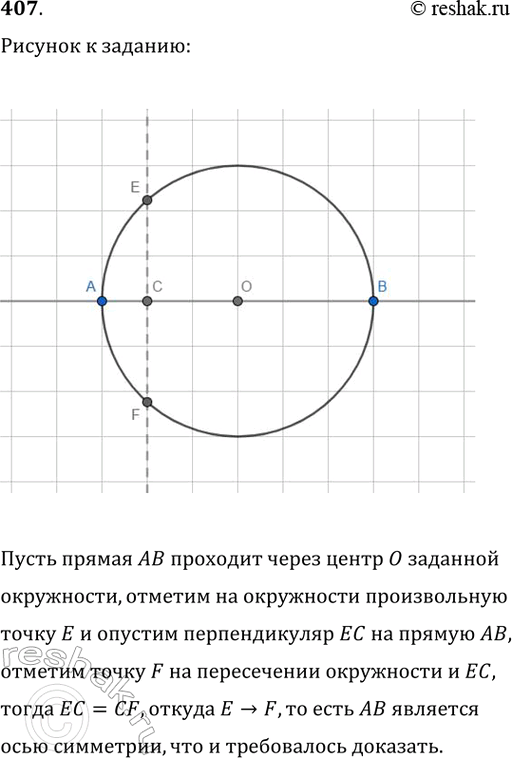
Докажите, что любая прямая, проходящая через центр окружности, является её осью симметрии.
Пусть прямая AB проходит через центр O заданной окружности, отметим на окружности произвольную точку E и опустим перпендикуляр EC на прямую AB, отметим точку F на пересечении окружности и EC, тогда EC=CF, откуда E > F, то есть AB является осью симметрии, что и требовалось доказать.
Задание учебника 2023 года
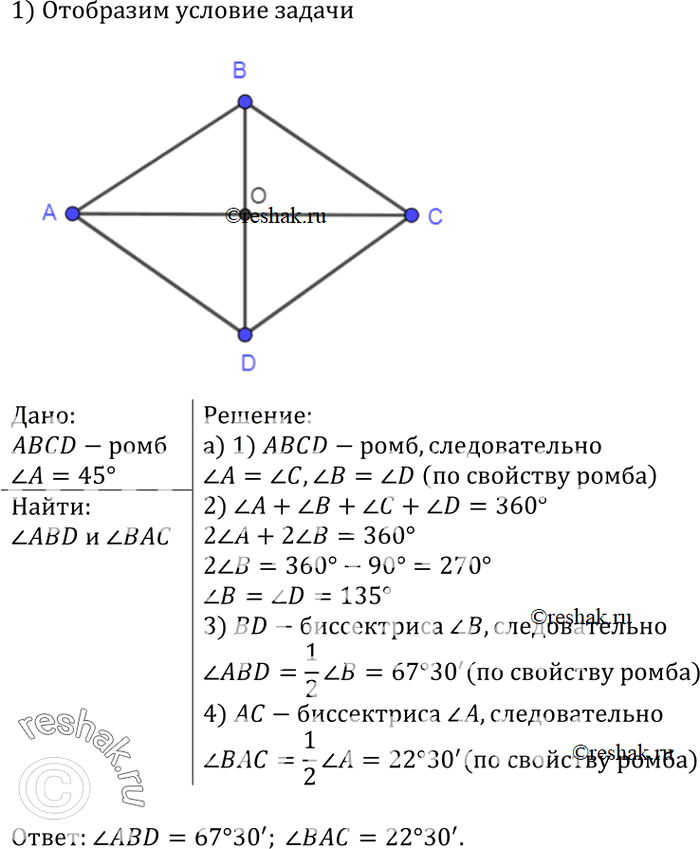
Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45°.
