Упр.404 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
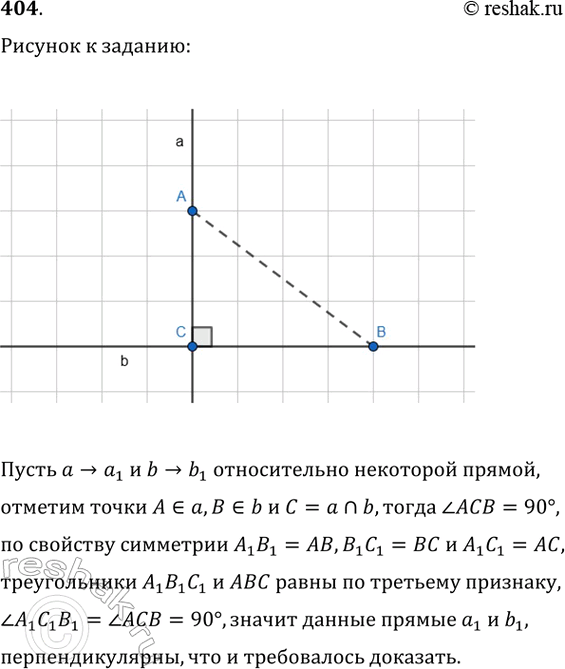
404. Докажите, что прямые, симметричные двум данным перпендикулярным прямым относительно прямой а, перпендикулярны.
Пусть a>a_1 и b>b_1 относительно некоторой прямой, отметим точки A принадлежит a,B принадлежит b и C=anb,тогда угол ACB=90°, по свойству симметрии A_1 B_1=AB,B_1 C_1=BC и A_1 C_1=AC, треугольники A_1 B_1 C_1 и ABC равны по третьему признаку, угол A_1 C_1 B_1=угол ACB=90°,значит данные прямые a_1 и b_1, перпендикулярны, что и требовалось доказать.
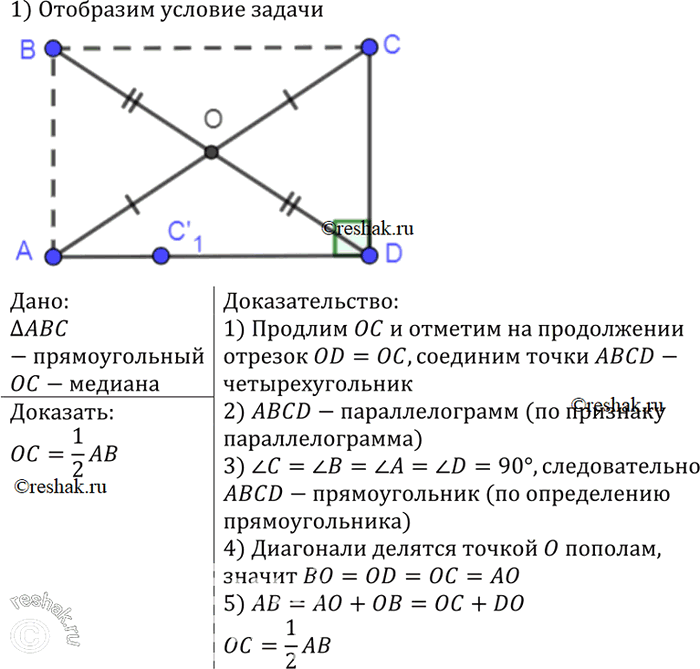
Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
Похожие решебники
Популярные решебники 7 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







