Упр.400 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
400. В равнобедренный треугольник вписана окружность с центром O_1, и около него описана окружность с центром O_2. Докажите, что точки O_1 и O_2 лежат на серединном перпендикуляре к основанию треугольника.
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, а центр описанной окружности лежит в точке пересечения серединных перпендикуляров треугольника, у равнобедренного треугольника медиана, проведенная к основанию, является также его высотой и биссектрисой, значит центры данных окружностей лежат на серединном перпендикуляре к основанию этого треугольника, что и требовалось доказать.
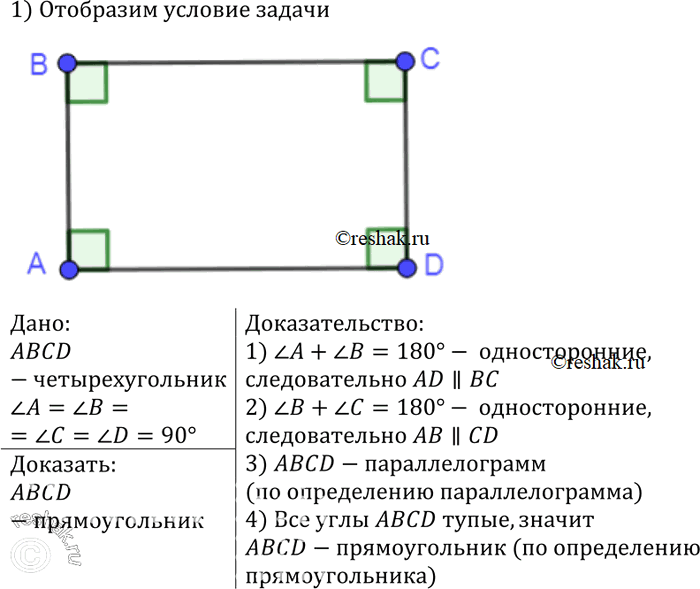
Докажите, что если в четырёхугольнике все углы прямые, то четырёхугольник — прямоугольник.
Похожие решебники
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением