Упр.398 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника
Атанасян, Бутузов 7 класс, Просвещение:
Задание учебника 2025 года
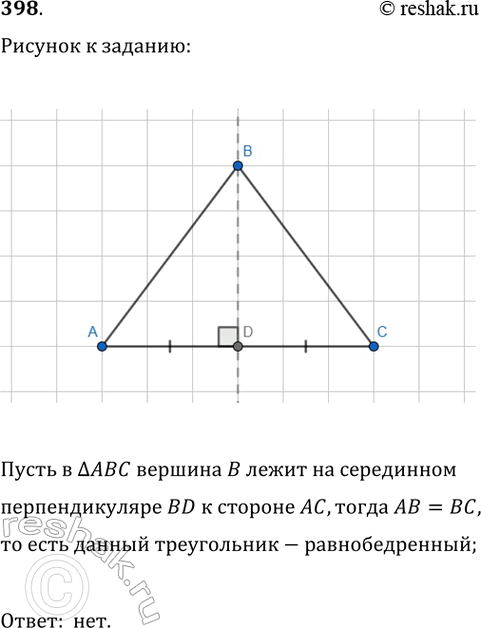
Может ли вершина разностороннего треугольника лежать на серединном перпендикуляре к какой-либо стороне? Ответ обоснуйте.
Пусть в треугольнике ABC вершина B лежит на серединном перпендикуляре BD к стороне AC, тогда AB=BC, то есть данный треугольник-равнобедренный;
Ответ: нет.
Задание учебника 2023 года
Постройте прямоугольную трапецию ABCD по основаниям и боковой стороне AD, перпендикулярной к основаниям.
