Упр.399 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
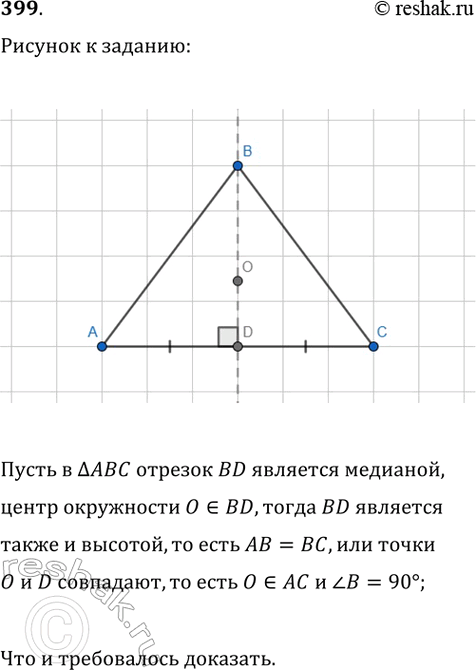
399. Центр описанной около треугольника окружности лежит на медиане. Докажите, что этот треугольник либо равнобедренный, либо прямоугольный.
Пусть в треугольнике ABC отрезок BD является медианой, центр окружности O принадлежит BD, тогда BD является также и высотой, то есть AB=BC, или точки O и D совпадают, то есть O принадлежит AC и угол B=90°. Что и требовалось доказать.
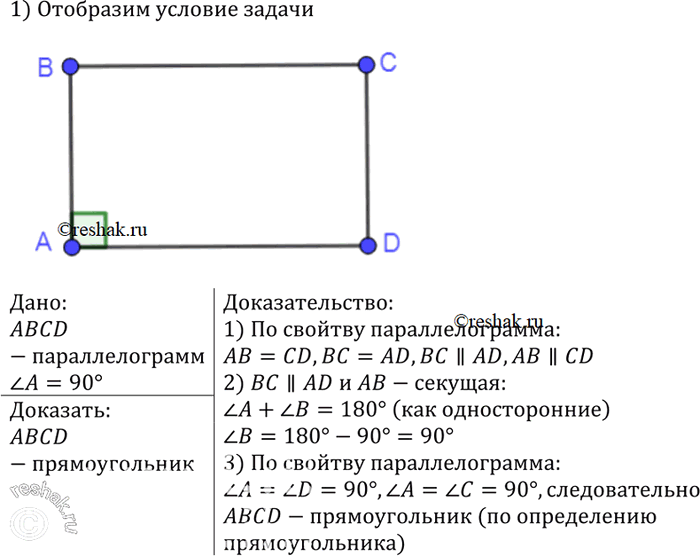
Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.
Похожие решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением