Упр.396 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)

Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
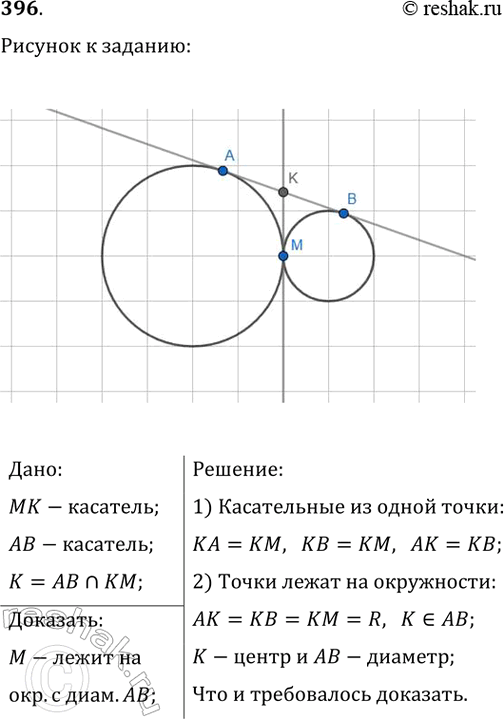
396*. Две окружности имеют общую точку М и общую касательную в этой точке. Прямая АВ касается одной окружности в точке А, а другой — в точке В. Докажите, что точка М лежит на окружности с диаметром АВ.
Дано:
MK-касатель;
AB-касатель;
K=ABnKM;
Доказать:
M-лежит на
окр.с диам.AB;
Решение:
1) Касательные из одной точки:
KA=KM, KB=KM, AK=KB;
2) Точки лежат на окружности:
AK=KB=KM=R, K принадлежит AB;
K-центр и AB-диаметр;
Что и требовалось доказать.
Разделите данный отрезок АВ на п равных частей.
Решение
Проведём луч АХ, не лежащий на прямой АВ, и на нём от точки А отложим последовательно п равных отрезков АА1, А1А2, ..., Аn-1Аn (рис. 167), т. е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (на рисунке 167 n = 5). Проведём прямую АnВ (точка Аn — конец последнего отрезка) и построим прямые, проходящие через точки А1, А2, ..., Аn-1 и параллельные прямой АnВ. Эти прямые пересекают отрезок АВ в точках В1, В2, ..., Вn-1, которые по теореме Фалеса (задача 385) делят отрезок АВ на n равных частей.
Похожие решебники
Популярные решебники 7 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







