Упр.348 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника
Атанасян, Бутузов 7 класс, Просвещение:
Задание учебника 2025 года
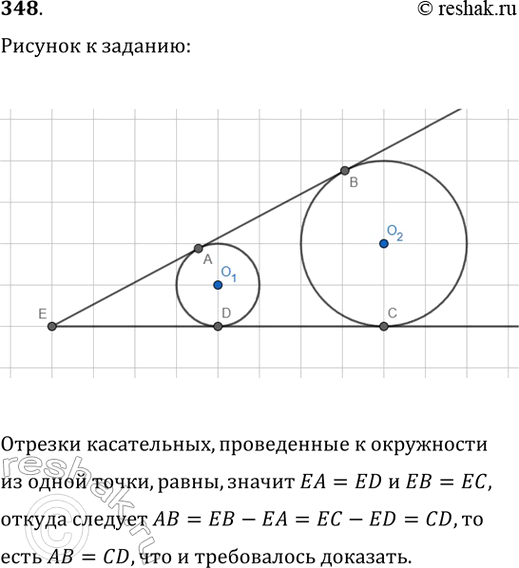
Две окружности с центрами О_1 и О_2 вписаны в угол. Одна из них касается его сторон в точках А и D, а вторая — в точках В и С. Докажите, что AB=CD.
Отрезки касательных, проведенные к окружности из одной точки, равны, значит EA=ED и EB=EC, откуда следует AB=EB-EA=EC-ED=CD, то есть AB=CD, что и требовалось доказать.
Задание учебника 2023 года
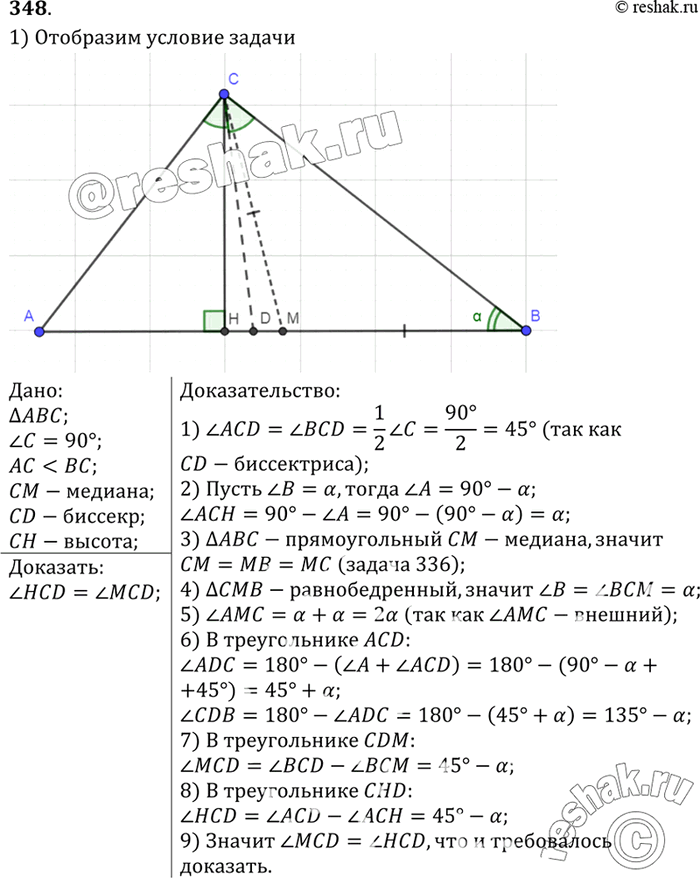
Докажите, что в прямоугольном треугольнике с неравными катетами биссектриса прямого угла делит угол между высотой и медианой, проведёнными из той же вершины, пополам.
