Упр.342 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1(Учебник 2025)
Решение #2(Учебник 2023)
Рассмотрим вариант решения задания из учебника
Атанасян, Бутузов 7-9 класс, Просвещение:
Задание учебника 2025 года
Докажите, что если хорды окружности равноудалены от её центра, то они равны.
Дано:
OF=OH;
OF перпендикулярно AC;
OH перпендикулярно DE;
Доказать:
AC=DE;
Решение:
1) В данной окружности:
OF перпендикулярно AC, отсюда AF=FC;
OH перпендикулярно DE, отсюда EH=HD;
2) По гипотенузе и катету:
OA=OE=R, OF=OH;
треугольник AFO=треугольник EHO, AF=EH;
AC=2•AF=2•EH=DE;
Что и требовалось доказать.
Задание учебника 2023 года
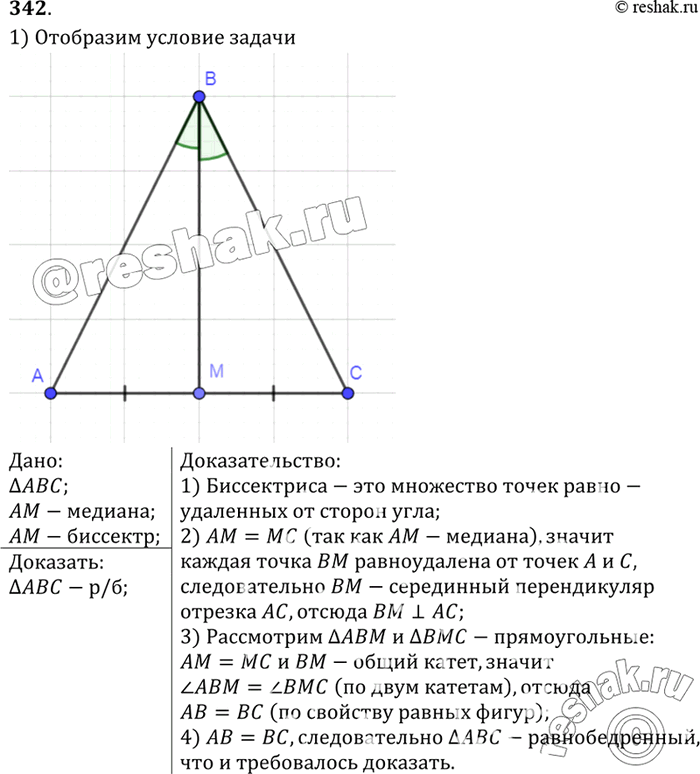
Докажите теорему: если в треугольнике биссектриса является медианой, то треугольник равнобедренный.
