Упр.346 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
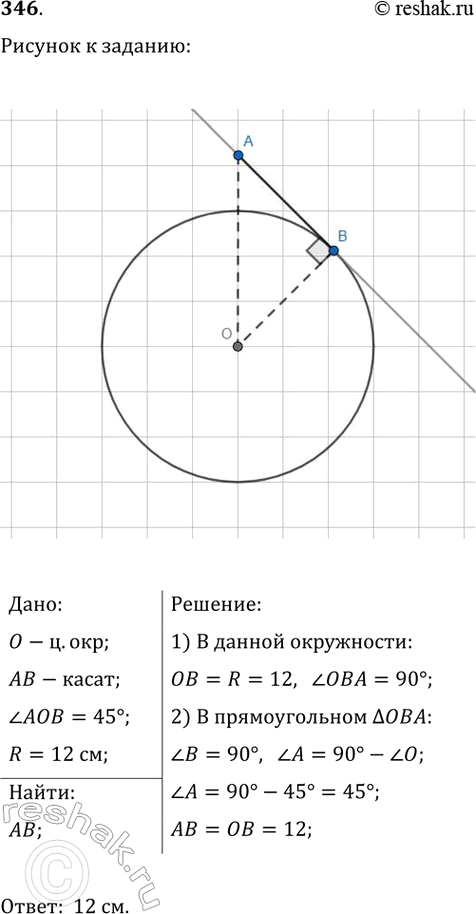
346. Найдите длину отрезка АВ, касательного к окружности с центром О, где В — точка касания, если угол АОВ равен 45°, а радиус окружности — 12 см.
Дано:
O-ц.окр;
AB-касат;
угол AOB=45°;
R=12 см;
Найти:
AB;
Решение:
1) В данной окружности:
OB=R=12, угол OBA=90°;
2) В прямоугольном треугольнике OBA:
угол B=90°, угол A=90°-угол O;
угол A=90°-45°=45°;
AB=OB=12;
Ответ: 12 см.
В треугольнике ABC, где АВ < АС, отрезок AD — биссектриса, отрезок АН — высота. Докажите, что точка Н лежит на луче DB.
Похожие решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением