Упр.334 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
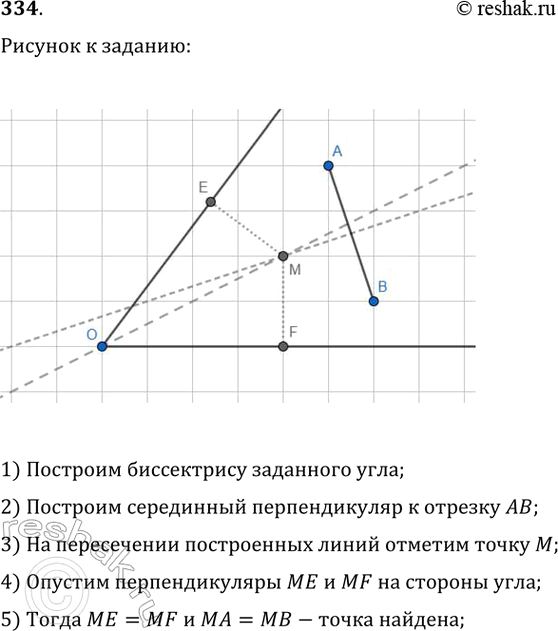
334. Даны угол и отрезок АВ. Постройте точку М, равноудалённую от сторон угла и такую, что MA=MB.
1) Построим биссектрису заданного угла;
2) Построим серединный перпендикуляр к отрезку AB;
3) На пересечении построенных линий отметим точку M;
4) Опустим перпендикуляры ME и MF на стороны угла;
5) Тогда ME=MF и MA=MB-точка найдена.
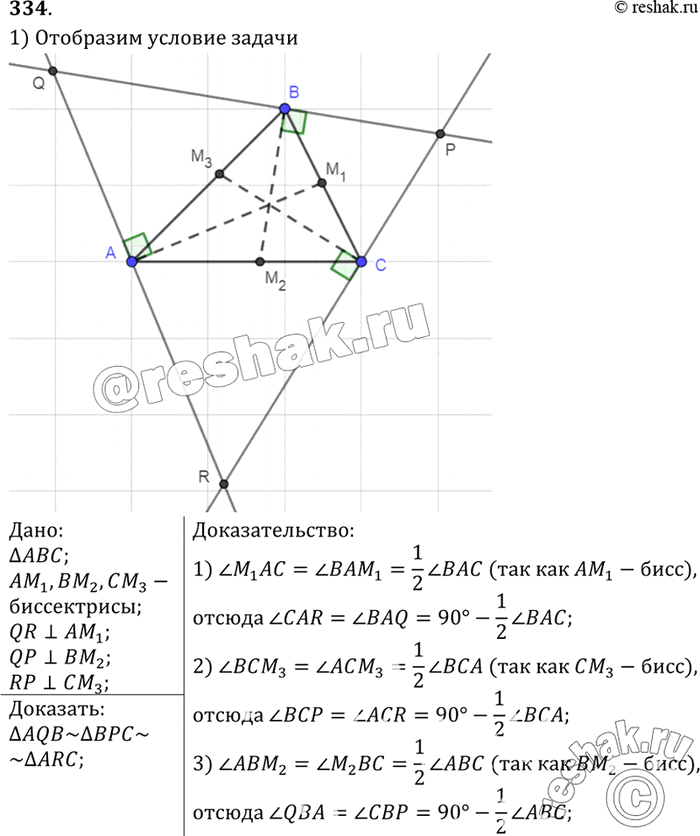
Через каждую вершину данного треугольника проведена прямая, перпендикулярная к биссектрисе треугольника, исходящей из этой вершины. Отрезки этих прямых вместе со сторонами данного треугольника образуют три треугольника. Докажите, что углы этих треугольников соответственно равны.
Похожие решебники
Популярные решебники 7 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







