Упр.331 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
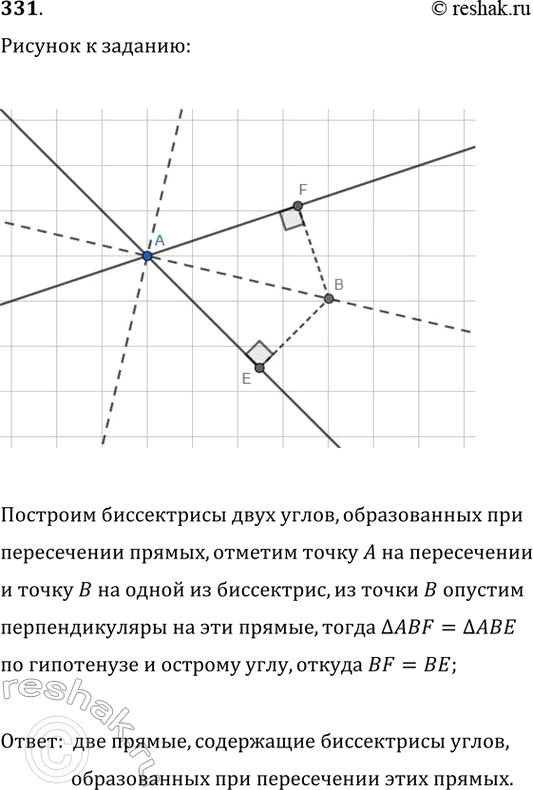
331. Определите геометрическое место всех точек плоскости, равноудалённых от двух пересекающихся прямых.
Построим биссектрисы двух углов, образованных при пересечении прямых, отметим точку A на пересечении и точку B на одной из биссектрис, из точки B опустим перпендикуляры на эти прямые, тогда треугольник ABF=треугольник ABE по гипотенузе и острому углу, откуда BF=BE;
Ответ: две прямые, содержащие биссектрисы углов, образованных при пересечении этих прямых.
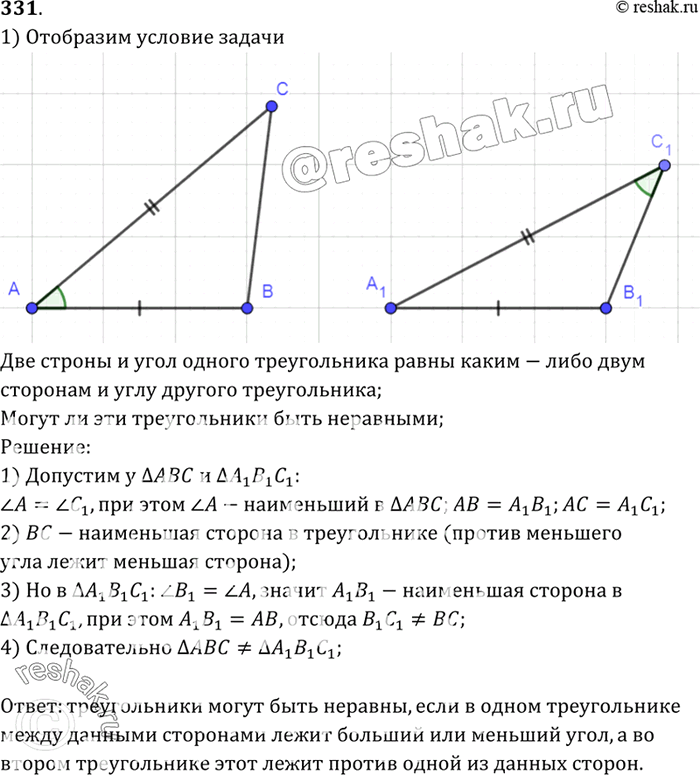
Две стороны и угол одного треугольника равны каким-то двум сторонам и углу другого треугольника. Могут ли эти треугольники быть неравными?
Похожие решебники
Популярные решебники 7 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







