Упр.1293 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)

Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 9 класс, Просвещение:
1293. Даны две пересекающиеся прямые и точка О, не лежащая ни на одной из них. Используя центральную симметрию, постройте прямую, проходящую через точку О, так, чтобы отрезок этой прямой, отсекаемый данными прямыми, делился точкой О пополам.
1) Пусть даны пересекающиеся прямые a и b и точка O;
2) Из точки O опустим перпендикуляр OE на прямую a;
3) Построим точку F симметрично E относительно O;
4) Через точку F проведем прямую параллельно a;
5) Отметим точку A не пересечении с прямой b;
6) Отметим точку B на пересечении AO и a;
7) Тогда, отрезок AB является искомым.
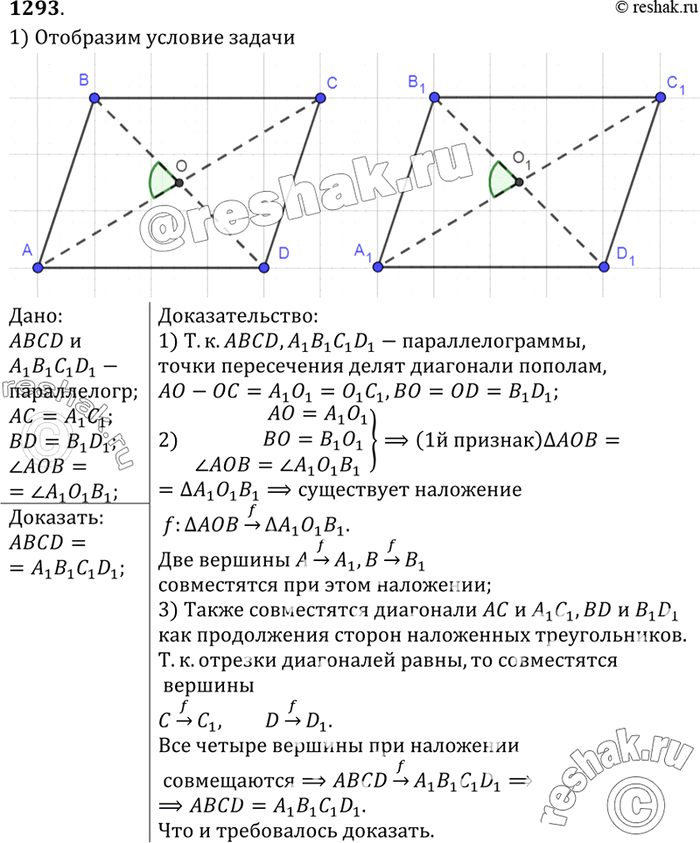
Докажите, что два параллелограмма равны, если диагонали и угол между ними одного параллелограмма соответственно равны диагоналям и углу между ними другого.
Похожие решебники
Популярные решебники 9 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







