Упр.796 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 8 класс, Просвещение:
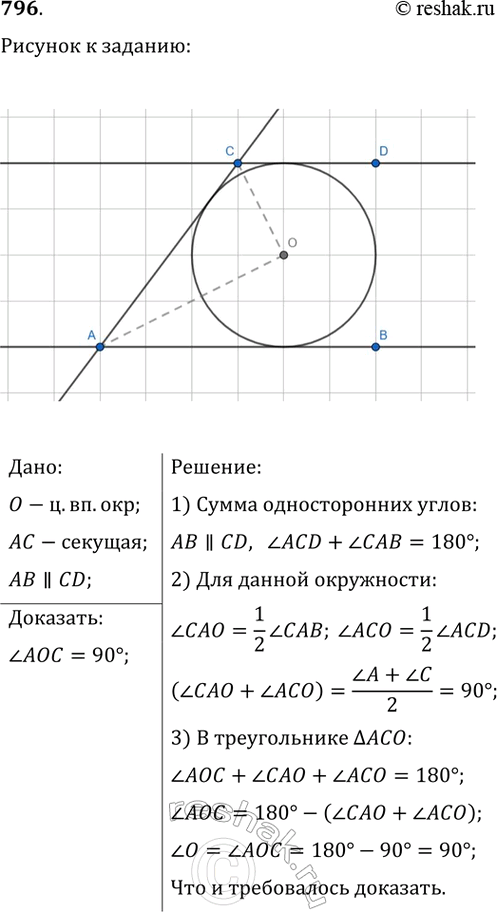
796. Окружность касается двух параллельных прямых и их секущей. Докажите, что отрезок секущей, заключённый между параллельными прямыми, виден из центра окружности под прямым углом (см. п. 41).
Дано:
O-ц.вп.окр;
AC-секущая;
AB || CD;
Доказать:
угол AOC=90°;
Решение:
1) Сумма односторонних углов:
AB || CD, угол ACD+угол CAB=180°;
2) Для данной окружности:
угол CAO=1/2угол CAB; угол ACO=1/2угол ACD;
(угол CAO+угол ACO)=(угол A+угол C)/2=90°;
3) В треугольнике ACO:
угол AOC+угол CAO+угол ACO=180°;
угол AOC=180°-(угол CAO+угол ACO);
угол O=угол AOC=180°-90°=90°;
Что и требовалось доказать.
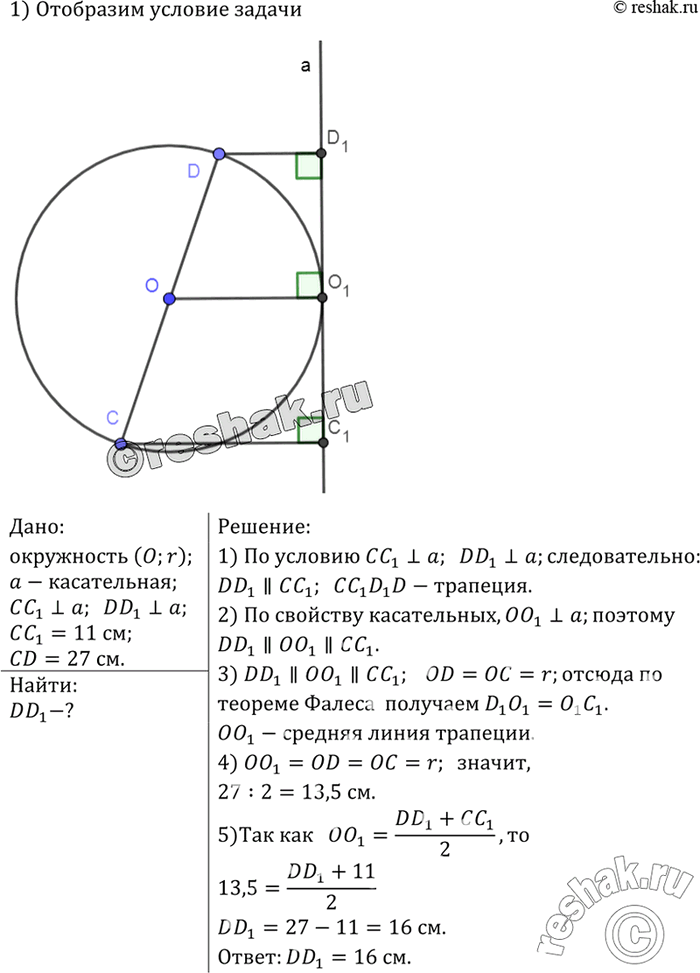
Из концов диаметра CD данной окружности проведены перпендикуляры СС1 и DD1 к касательной, не перпендикулярной к диаметру CD. Найдите DD1 если СС1 = 11 см, a CD = 27 см.
Похожие решебники
Популярные решебники 8 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







