Упр.794 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника
Атанасян, Бутузов 8 класс, Просвещение:
Задание учебника 2025 года
794. Докажите, что если в четырёхугольник можно вписать окружность, то её центр является точкой пересечения биссектрис углов этого четырёхугольника.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, вписанная в четырехугольник окружность касается каждой из его сторон, то есть она вписана в каждый из четырех углов, её центр лежит на всех биссектрисах четырехугольника, он лежит в точке их пересечения, что и требовалось доказать.
Задание учебника 2023 года
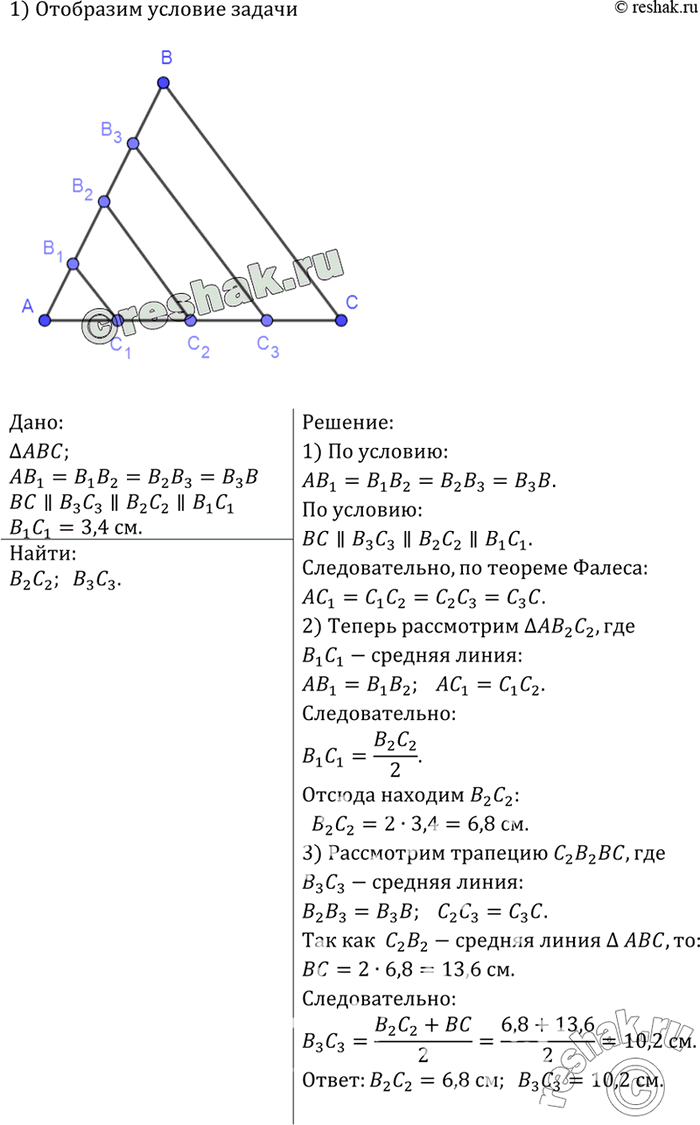
Сторона АВ треугольника ABC разделена на четыре равные части и через точки деления проведены прямые, параллельные стороне ВС. Стороны АВ и АС треугольника отсекают на этих параллельных прямых три отрезка, наименьший из которых равен 3,4 см. Найдите два других отрезка.
