Упр.758 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 8 класс, Просвещение:
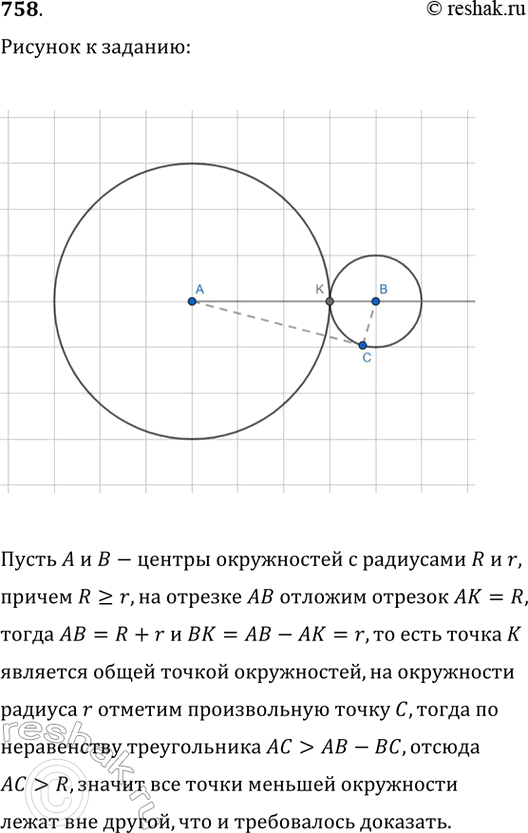
758. Докажите утверждение 2 из теоремы о взаимном расположении окружностей: если расстояние между центрами двух окружностей равно сумме радиусов этих окружностей, то окружности касаются внешним образом.
Пусть A и B-центры окружностей с радиусами R и r, причем R>=r,на отрезке AB отложим отрезок AK=R, тогда AB=R+r и BK=AB-AK=r, то есть точка K является общей точкой окружностей, на окружности
радиуса r отметим произвольную точку C, тогда по неравенству треугольника AC>AB-BC, отсюда AC>R, значит все точки меньшей окружности лежат вне другой, что и требовалось доказать.
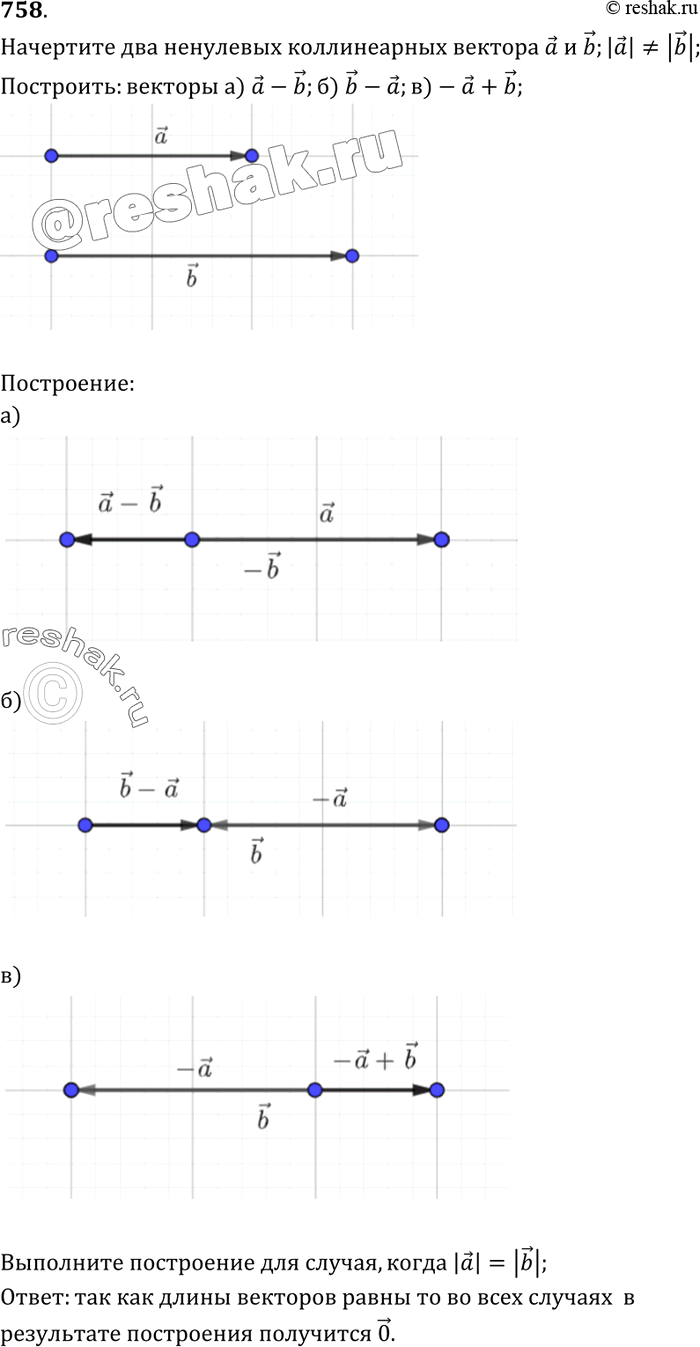
Начертите два ненулевых коллинеарных вектора а и b так, чтобы |а| не равен |b|. Постройте векторы: а а - b; б) b - а; в) -а + b. Выполните ещё раз построение для случая, когда |а| = |b|.
Похожие решебники
Популярные решебники 8 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







