Упр.489 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 8 класс, Просвещение:
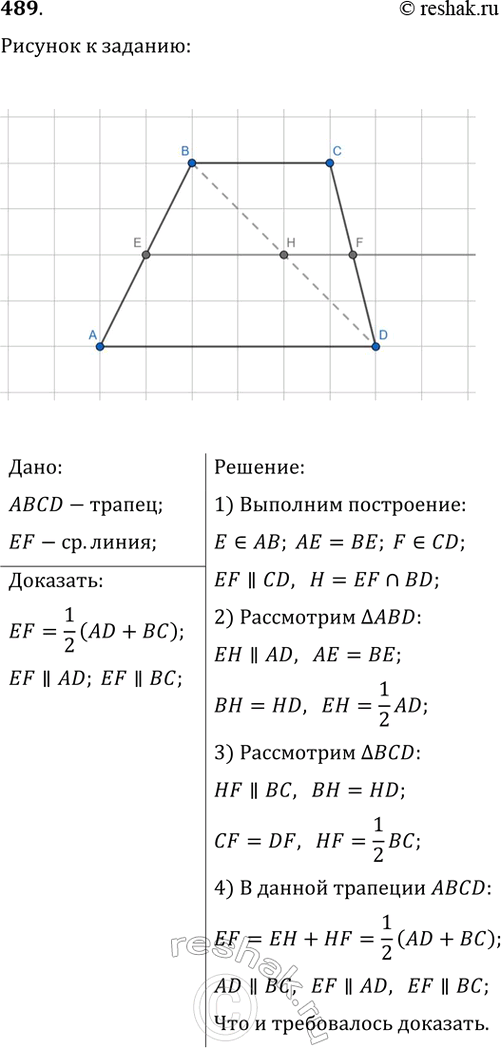
489. Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. Докажите свойство средней линии трапеции: средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
Дано:
ABCD-трапец;
EF-ср.линия;
Доказать:
EF=1/2 (AD+BC);
EF || AD; EF || BC;
Решение:
1) Выполним построение:
E принадлежит AB; AE=BE; F принадлежит CD;
EF || CD, H=EFnBD;
2) Рассмотрим треугольник ABD:
EH || AD, AE=BE;
BH=HD, EH=1/2 AD;
3) Рассмотрим треугольник BCD:
HF || BC, BH=HD;
CF=DF, HF=1/2 BC;
4) В данной трапеции ABCD:
EF=EH+HF=1/2 (AD+BC);
AD || BC, EF || AD, EF || BC;
Что и требовалось доказать.
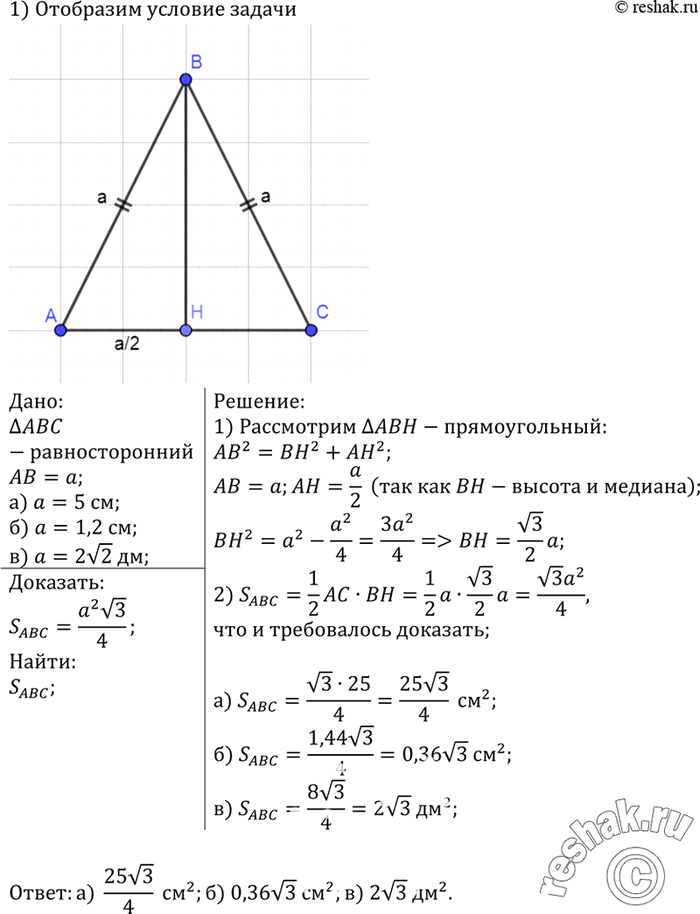
Докажите, что площадь равностороннего треугольника вычисляется по формуле S = a2корень3/4, где а — сторона треугольника. Найдите площадь равностороннего треугольника, если его сторона равна: а) 5 см; б) 1,2 см; в) 2корень2 дм.
Похожие решебники
Популярные решебники 8 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







