Упр.486 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 8 класс, Просвещение:
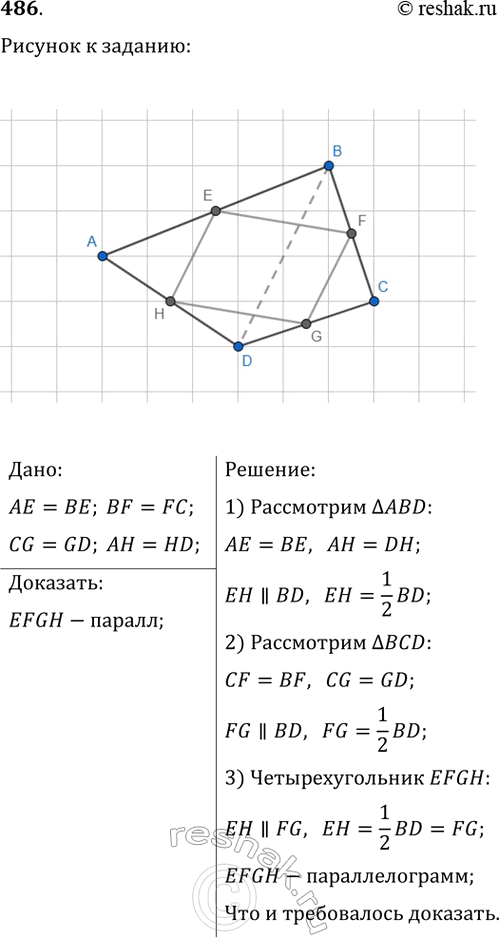
486. Докажите, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма (теорема Вариньона).
Дано:
AE=BE; BF=FC;
CG=GD; AH=HD;
Доказать:
EFGH-паралл;
Решение:
1) Рассмотрим треугольник ABD:
AE=BE, AH=DH;
EH || BD, EH=1/2 BD;
2) Рассмотрим треугольник BCD:
CF=BF, CG=GD;
FG || BD, FG=1/2 BD;
3) Четырехугольник EFGH:
EH || FG, EH=1/2 BD=FG;
EFGH-параллелограмм;
Что и требовалось доказать.
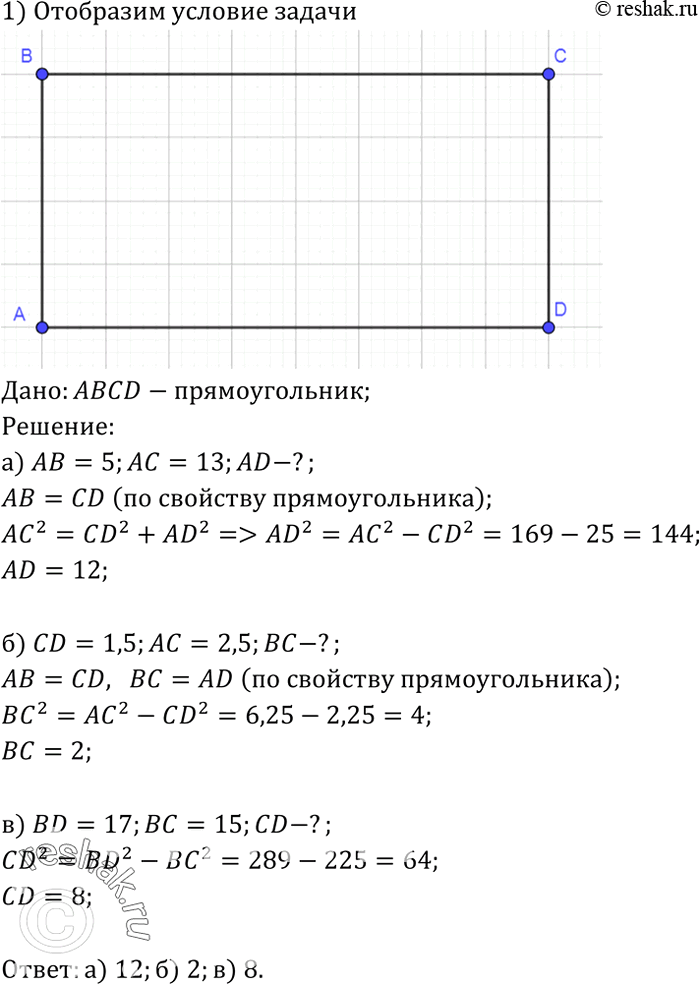
В прямоугольнике ABCD найдите:
а) AD, если АВ = 5, АС =13;
б) ВС, если CD= 1,5, АС = 2,5;
в) CD, если BD= 17, ВС= 15.
Похожие решебники
Популярные решебники 8 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением