Упр.2.60 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
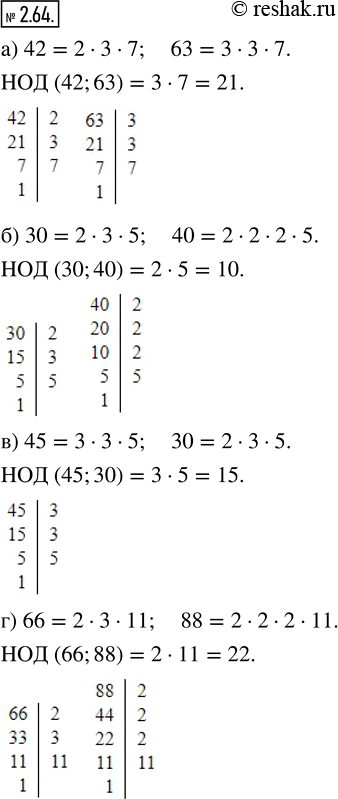
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
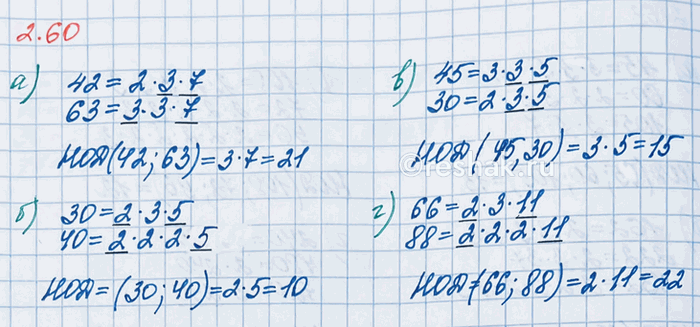
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите наибольший общий делитель чисел:
а) 42 и 63; б) 30 и 40; в) 45 и 30; г) 66 и 88.
а) Разложим числа 42 и 63 на простые множители и подчеркнём общие множители чисел.
42=2•3•7
63=3•3•7
Общие множители чисел: 3; 7.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (42;63)=3•7=21
б) Разложим числа 30 и 40 на простые множители и подчеркнём общие множители чисел.
30=2•3•5
40=2•2•2•5
Общие множители чисел: 2; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (30;40)=2•5=10
в) Разложим числа 45 и 30 на простые множители и подчеркнём общие множители чисел.
45=3•3•5
30=2•3•5
Общие множители чисел: 3; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (45;30)=3•5=15
г) Разложим числа 66 и 88 на простые множители и подчеркнём общие множители чисел.
66=2•3•11
88=2•2•2•11
Общие множители чисел: 2; 11.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (66;88)=2•11=22
Вычислите:
а) 51 - (3,75 : 3 + 86,45 : 24,7) · 2,4; б) (650 000 : 3125 - 196,5) · 3,14.
Если в выражении есть скобки, то сначала выполняют действия в скобках.
Если выражение содержит действия первой и второй ступени, то сначала выполняют действия второй ступени по порядку слева направо, а потом действия первой ступени, также по порядку слева направо.
При этом сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.
Над примерами расставим цифрами порядок действий.
а) 51-(3,75:3+86,45:24,7)•2,4=51-(1,25+86,45:24,7)•2,4=51-(1,25+864,5:247)•2,4=51-(1,25+3,5)•2,4=51-4,75•2,4=51-11,4=39,6
б) (650 000:3 125-196,5)•3,14=(208-196,5)•3,14=11,5•3,14=36,11
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.