Упр.2.57 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)



Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
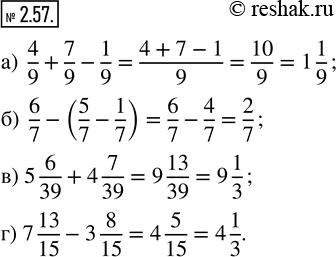
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите все общие делители чисел:
а) 20 и 70; б) 36, 48 и 144; в) 22 и 105.
а) 20 и 70
Для того, чтобы определить общие делители чисел, необходимо знать все делители числа 20 и все делители числа 70.
Для того, чтобы определить делители числа, необходимо знать на какие простые множители можно разложить данное число.
20=2•2•5
Перебираем простые множители, сочетаем их с друг другом.
Так находим все делители числа 20 (1 и само число также делители).
1, 2, 4, 5, 10, 20.
Затем с помощью простых множителей числа 70 находим все делители числа 70.
70=2•5•7
1, 2, 5, 7, 10, 14, 35, 70.
Общие делители (ОД) чисел 20 и 70 – это те числа, которые встречаются среди делителей числа 20 и среди делителей числа 70.
ОД(20,70)=1,2,5,10.
б) 36, 48 и 144
Для того, чтобы определить общие делители чисел, необходимо знать все делители числа 36, все делители числа 48 и все делители числа 144.
Для того, чтобы определить делители числа, необходимо знать на какие простые множители можно разложить данное число.
36=2•2•3•3
Перебираем простые множители, сочетаем их с друг другом.
Так находим все делители числа 36 (1 и само число также делители).
1, 2, 3, 4, 6, 9, 12, 18, 36.
Затем с помощью простых множителей числа 48 находим все делители числа 48.
48=2•2•2•2•3
1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
Затем с помощью простых множителей числа 144 находим все делители числа 144.
144=2•2•2•2•3•3
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144.
Общие делители (ОД) чисел 36, 48 и 144 – это те числа, которые встречаются среди делителей числа 36, среди делителей числа 48 и среди делителей числа 144.
ОД(36,48,144)=1,2,3,4,6,12.
в) 22 и 105
Для того, чтобы определить общие делители чисел, необходимо знать все делители числа 22 и все делители числа 105.
Для того, чтобы определить делители числа, необходимо знать на какие простые множители можно разложить данное число.
22=2•11
Перебираем простые множители, сочетаем их с друг другом.
Так находим все делители числа 22 (1 и само число также делители).
1, 2, 11, 22.
Затем с помощью простых множителей числа 105 находим все делители числа 105.
105=3•5•7
1, 3, 5, 7, 15, 21, 35, 105.
Общие делители (ОД) чисел 22 и 105 – это те числа, которые встречаются среди делителей числа 22 и среди делителей числа 105.
ОД(22,105)=1.
Найдите значение выражения:
а) 4/9 + 7/9 - 1/9; б) 6/7 - (5/7 - 1/7); в) 5 6/39 + 4 7/39; г) 7 13/15 - 3 8/15.
При сложении (вычитании) дробей с одинаковыми знаменателями получаем дробь с тем же знаменателем, а в числителе будет значение суммы (разности) прежних числителей (числители складывают (вычитают), а знаменатель остаётся тот же).
При сложении (вычитании) чисел в смешанной записи целые части складывают (вычитают) отдельно, а дробные – отдельно.
а) 4/9+7/9-1/9=(4+7-1)/9=10/9=1 1/9
Дробь 10/9 - неправильная, необходимо выделить целую часть.
Для этого числитель делим на знаменатель с остатком.
10:9=1 целая и 1 в остатке.
В ответе получаем число 1 1/9.
б) 6/7-(5/7-1/7)=6/7-5/7+1/7=(6-5+1)/7=2/7
в) 5 6/39+4 7/39=(5+6/39)+(4+7/39)=(5+4)+(6/39+7/39)=9+(6+7)/39=9+13/39=9+(13•1)/(13•3)=9+1/3=9 1/3
г) 7 13/15-3 8/15=(7+13/15)-(3+8/15)=(7-3)+(13/15-8/15)=4+(13-8)/15=4+5/15=4+(5•1)/(5•3)=4+1/3=4 1/3
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.