Упр.2.66 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
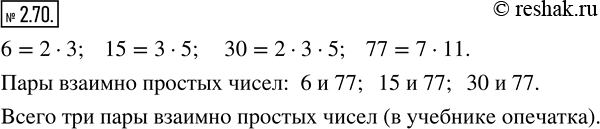
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
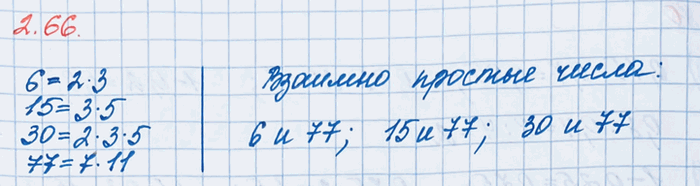
Решение #4 (Учебник 2021)
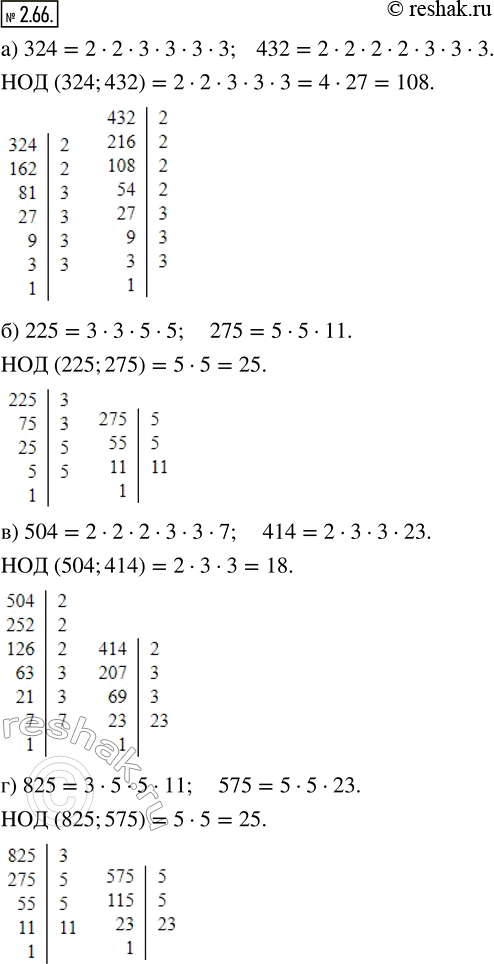
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)
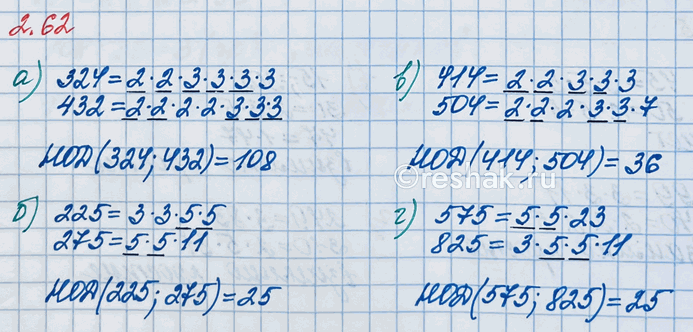
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Среди чисел 6, 15, 30 и 77 найдите четыре пары взаимно простых чисел.
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Значит, необходимо найти среди данных чисел такие пары, чей наибольший общий делитель равен 1 (то есть эти числа при разложении на простые множители не будут иметь одинаковых множителей).
Раскладываем каждое число на простые множители.
6=2•3
15=3•5
30=2•3•5
77=7•11
Видим, какие пары чисел не имеют общих простых множителей:
6 и 77; 15 и 77; 30 и 77.
Найдите наибольший общий делитель чисел:
а) 324 и 432; б) 225 и 275; в) 504 и 414; г) 825 и 575.
а) Разложим числа 324 и 432 на простые множители и подчеркнём общие множители чисел.
324=2•2•3•3•3•3
432=2•2•2•2•3•3•3
Общие множители чисел: 2; 2; 3; 3; 3.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (324;432)=2•2•3•3•3=4•27=108
б) Разложим числа 225 и 275 на простые множители и подчеркнём общие множители чисел.
225=3•3•5•5
275=5•5•11
Общие множители чисел: 5; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (225;275)=5•5=25
в) Разложим числа 504 и 414 на простые множители и подчеркнём общие множители чисел.
504=2•2•2•3•3•7
414=2•3•3•23
Общие множители чисел: 2; 3; 3.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (504;414)=2•3•3=6•3=18
г) Разложим числа 825 и 575 на простые множители и подчеркнём общие множители чисел.
825=3•5•5•11
575=5•5•23
Общие множители чисел: 5; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (825;575)=5•5=25
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









