Упр.2.59 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
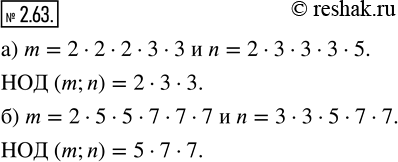
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
Решение #5 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Назовите наибольший общий делитель чисел m и n в виде разложения на простые множители, если:
а) m = 2 · 2 · 2 · 3 · 3 и n = 2 · 3 · 3 · 3 · 5;
б) m = 2 · 5 · 5 · 7 · 7 · 7 и n = 3 · 3 · 5 · 7 · 7.
Наибольшим общим делителем (НОД) нескольких чисел называют наибольшее натуральное число, на которое делятся эти числа без остатка.
Для того, чтобы найти наибольший общий делитель нескольких натуральных чисел, необходимо:
- разложить их на простые множители;
- из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые входят в разложение других чисел;
- найти произведение этих множителей.
а) m=2•2•2•3•3
n=2•3•3•3•5
НОД (m,n)=2•3•3
б) m=2•5•5•7•7•7
n=3•3•5•7•7
НОД (m,n)=5•7•7
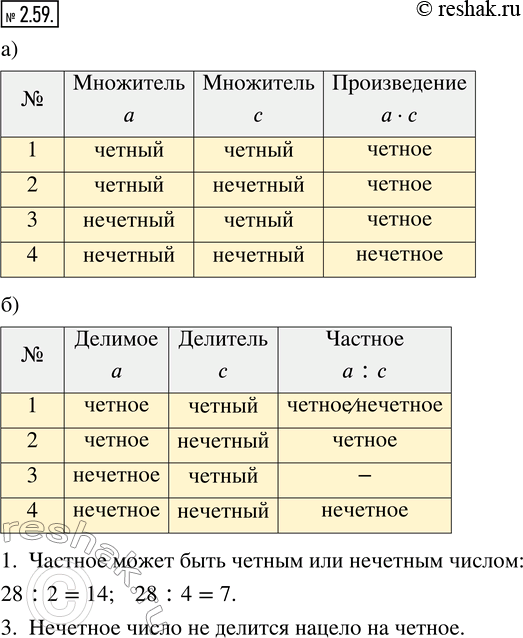
Определите чётным или нечётным числом будет результат действия в каждом случае (а, с и a : с — натуральные числа).
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.