Упр.2.65 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1
Решение #2
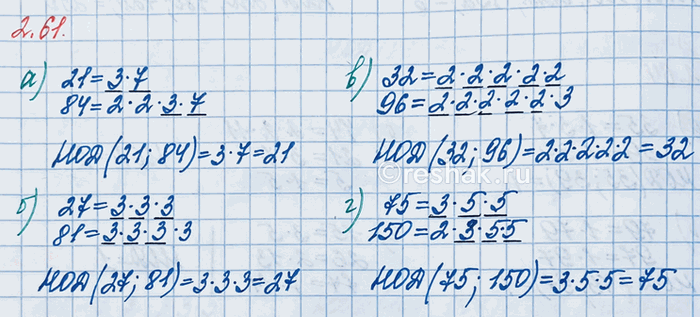
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
2.65. Найдите наибольший общий делитель чисел:
а) 21 и 84; б) 27 и 81; в) 32 и 96; г) 75 и 300.
а) Разложим числа 21 и 84 на простые множители и подчеркнём общие множители чисел.
21=3•7
84=2•2•3•7
Общие множители чисел: 3; 7.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (21;84)=3•7=21
б) Разложим числа 27 и 81 на простые множители и подчеркнём общие множители чисел.
27=3•3•3
81=3•3•3•3
Общие множители чисел: 3; 3; 3.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (27;81)=3•3•3=9•3=27
в) Разложим числа 32 и 96 на простые множители и подчеркнём общие множители чисел.
32=2•2•2•2•2
96=2•2•2•2•2•3
Общие множители чисел: 2; 2; 2; 2; 2.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (32;96)=2•2•2•2•2=8•4=32
г) Разложим числа 75 и 300 на простые множители и подчеркнём общие множители чисел.
75=3•5•5
300=2•2•3•5•5
Общие множители чисел: 3; 5; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (75;300)=3•5•5=3•25=75
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
