Упр.2.469 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)
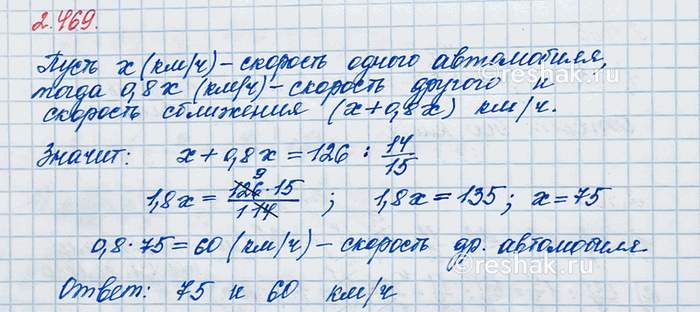
Решение #3 (Учебник 2021)
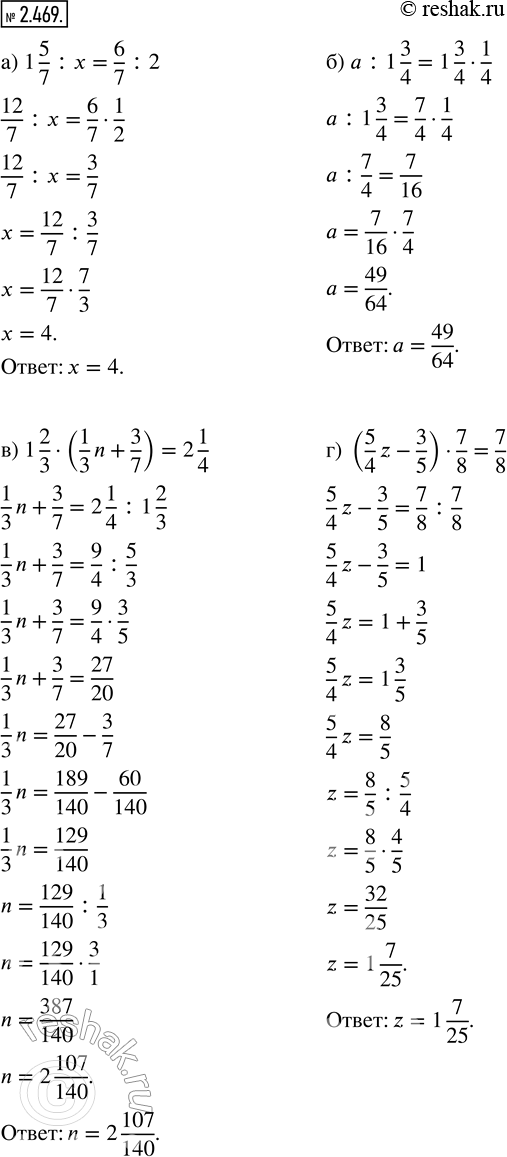
Решение #4 (Учебник 2021)





Решение #5 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Сейчас между автомобилями, движущимися навстречу друг другу, 126 км, и встретятся они через 14/15 ч. Найдите скорость каждого автомобиля, если скорость одного из них составляет 80 % скорости другого.
Решите уравнение:
а) 1 5/7 : x = 6/7 : 2; в) 1 2/3 · (1/3 x + 3/7) = 2 1/4;
б) a : 1 3/4 = 1 3/4 · 1/4; г) (5/4 z - 3/5) · 7/8 = 7/8.
При вычислениях опираемся на следующие правила:
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение (деление) смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения (деления) дробей.
При этом, прежде, чем перемножить числа, выполняем сокращение.
- для того, чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
- для того, чтобы сложить (вычесть) дроби с разными знаменателями, необходимо привести данные дроби к наименьшему общему знаменателю, а затем сложить (вычесть) полученные дроби.
- для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать, как целую часть смешанного числа, а остаток – как числитель его дробной части.
- для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
а) 1 5/7 :x=6/7 :2
12/7 :x=6/7 :2/1
12/7 :x=6/7•1/2
12/7 :x=(6•1)/(7•2)
12/7 :x=(2•3)/(7•2)
12/7 :x=3/7
Неизвестен делитель x.
Для того, чтобы найти неизвестный делитель, необходимо делимое разделить на частное, получим
x=12/7 :3/7
x=12/7•7/3
x=(12•7)/(7•3)
x=(3•4•7)/(7•3)
x=4/1
x=4
б) a:1 3/4=1 3/4•1/4
a:7/4=7/4•1/4
a:7/4=(7•1)/(4•4)
a:7/4=7/16
Неизвестно делимое a.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим
a=7/16•7/4
a=(7•7)/(16•4)
a=49/64
в) 1 2/3•(1/3 n+3/7)=2 1/4
Решаем уравнение относительно произведения, то есть неизвестен множитель 1/3 n+3/7 .
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
1/3 n+3/7=2 1/4 :1 2/3
1/3 n+3/7=9/4 :5/3
1/3 n+3/7=9/4•3/5
1/3 n+3/7=(9•3)/(4•5)
1/3 n+3/7=27/20
Теперь решаем уравнение относительно сложения, то есть неизвестно слагаемое 1/3 n.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
1/3 n=27/20-3/7
1/3 n=(27•7)/(20•7)-(3•20)/(7•20)
1/3 n=189/140-60/140
1/3 n=(189-60)/140
1/3 n=129/140
Теперь решаем уравнение относительно произведения, то есть неизвестен множитель n.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
n=129/140 :1/3
n=129/140•3/1
n=(129•3)/140
n=387/140
n=2 107/140
г) (5/4 z-3/5)•7/8=7/8
Решим уравнение относительно произведения, то есть неизвестен множитель 5/4 z-3/5 .
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
5/4 z-3/5=7/8 :7/8
5/4 z-3/5=1
Теперь решаем уравнение относительно вычитания, то есть неизвестно уменьшаемое 5/4 z.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
5/4 z=1+3/5
5/4 z=1 3/5
Решаем уравнение относительно произведения, то есть неизвестен множитель z.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
z=1 3/5 :5/4
z=8/5 :5/4
z=8/5•4/5
z=(8•4)/(5•5)
z=32/25
z=1 7/25
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением








