Упр.2.466 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
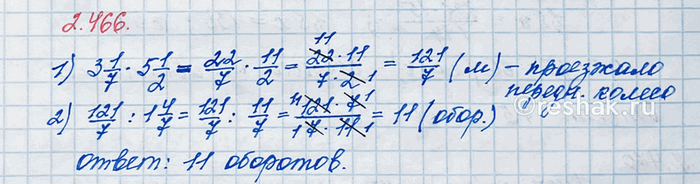
Решение #4 (Учебник 2021)
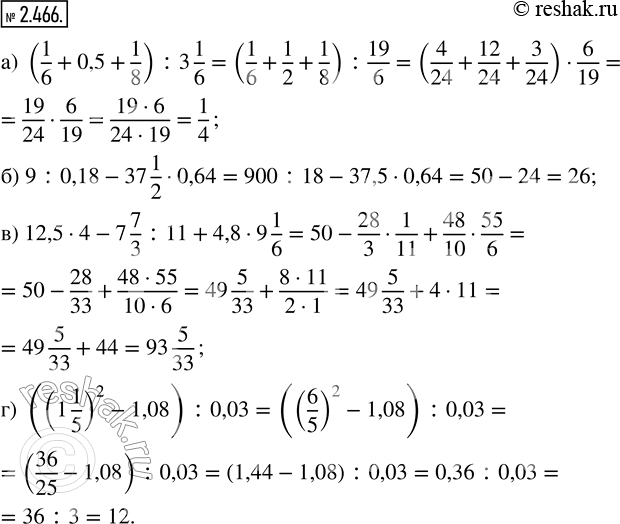
Решение #5 (Учебник 2021)


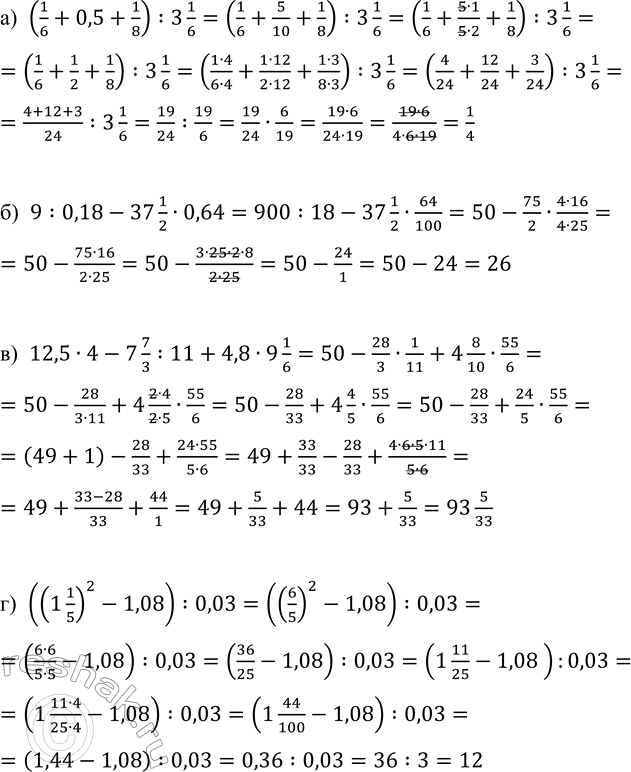
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
У велосипеда, изобретённого крепостным уральским мастером Ефимом Артамоновым в 1800 г., переднее колесо было больше заднего. Длина окружности переднего колеса была равна 3 1/7 м, а заднего — 1 4/7 м. Сколько оборотов делало заднее колесо за 5 1/2 оборота переднего колеса?
Для начала определим, какое расстояние проезжает переднее колесо за 5 1/2 оборота.
Для этого необходимо количество проделанных оборотов умножить на длину окружности переднего колеса.
5 1/2•3 1/7=11/2•22/7=(11•22)/(2•7)=(11•2•11)/(2•7)=121/7=17 2/7 м.
Для того, чтобы выполнить умножение (деление) смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения (деления) дробей.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Для того, чтобы найти, сколько оборотов сделает колесо на заданном расстоянии, если известна длина окружности колеса, необходимо разделить заданное расстояние на длину окружности колеса.
Таким образом, заднее колесо сделает
17 2/7 :1 4/7=121/7 :11/7=121/7•7/11=(121•7)/(7•11)=(11•11•7)/(7•11)=11/1=11 оборотов.
Для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
Ответ: 11 оборотов.
Вычислите:
а) (1/6 + 0,5 + 1/8) : 3 1/6; в) 12,5 · 4 - 7 7/3 : 11 + 4,8 · 9 1/6;
б) 9 : 0,18 - 37 1/2 · 0,64; г) ((1 1/5)^2 - 1,08) : 0,03.
Порядок выполнения действий выбираем согласно следующим правилам:
- если в выражении нет скобок, и оно содержит действия первой (сложение и вычитание) и второй ступени (умножение и деление), то сначала выполняют действия второй ступени по порядку
- если в выражении есть скобки, то сначала выполняют действия в скобках, а затем за скобками.
- и в скобках, и за скобками сначала выполняются действия умножения и деления, а затем сложения и вычитания, по порядку слева направо.
При вычислениях опираемся на следующие правила:
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение (деление) смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения (деления) дробей.
При этом, прежде, чем перемножить числа, выполняем сокращение.
- для того, чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
- для того, чтобы сложить (вычесть) дроби с разными знаменателями, необходимо привести данные дроби к наименьшему общему знаменателю, а затем сложить (вычесть) полученные дроби.
- для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать, как целую часть смешанного числа, а остаток – как числитель его дробной части.
- для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
а) (1/6+0,5+1/8) :3 1/6=(1/6+5/10+1/8) :3 1/6=(1/6+(5•1)/(5•2)+1/8) :3 1/6=(1/6+1/2+1/8) :3 1/6=((1•4)/(6•4)+(1•12)/(2•12)+(1•3)/(8•3)) :3 1/6=(4/24+12/24+3/24) :3 1/6=(4+12+3)/24 :3 1/6=19/24 :19/6=19/24•6/19=(19•6)/(24•19)=(19•6)/(4•6•19)=1/4
б) 9:0,18-37 1/2•0,64=900:18-37 1/2•64/100=50-75/2•(4•16)/(4•25)=50-(75•16)/(2•25)=50-(3•25•2•8)/(2•25)=50-24/1=50-24=26
в) 12,5•4-7 7/3 :11+4,8•9 1/6=50-28/3•1/11+4 8/10•55/6=50-28/(3•11)+4 (2•4)/(2•5)•55/6=50-28/33+4 4/5•55/6=50-28/33+24/5•55/6=(49+1)-28/33+(24•55)/(5•6)=49+33/33-28/33+(4•6•5•11)/(5•6)=49+(33-28)/33+44/1=49+5/33+44=93+5/33=93 5/33
г) ((1 1/5)^2-1,08) :0,03=((6/5)^2-1,08) :0,03=((6•6)/(5•5)-1,08) :0,03=(36/25-1,08) :0,03=(1 11/25-1,08 ):0,03==(1 (11•4)/(25•4)-1,08) :0,03=(1 44/100-1,08) :0,03=(1,44-1,08) :0,03=0,36:0,03=36:3=12
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением








