Упр.897 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1(Учебник 2025)
Решение #2(Учебник 2023)
Рассмотрим вариант решения задания из учебника
Атанасян, Бутузов 7-9 класс, Просвещение:
Задание учебника 2025 года
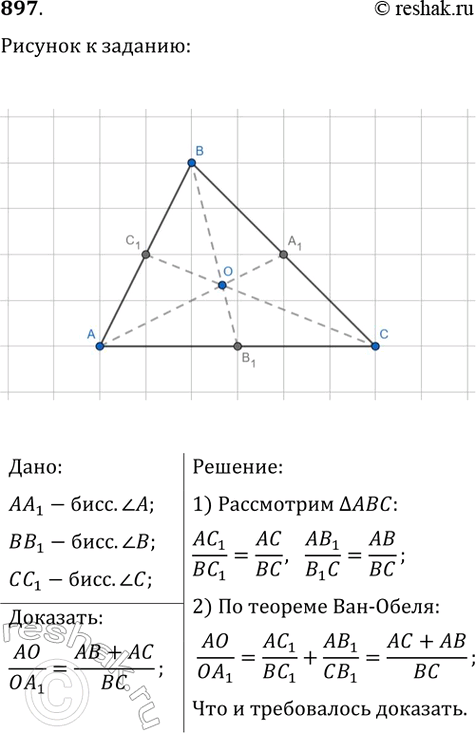
Докажите, что каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
Дано:
AA_1-бисс.угол A;
BB_1-бисс.угол B;
CC_1-бисс.угол C;
Доказать:
AO/(OA_1 )=(AB+AC)/BC;
Решение:
1) Рассмотрим треугольник ABC:
(AC_1)/(BC_1)=AC/BC, (AB_1)/(B_1 C)=AB/BC;
2) По теореме Ван-Обеля:
AO/(OA_1)=(AC_1)/(BC_1)+(AB_1)/(CB_1)=(AC+AB)/BC;
Что и требовалось доказать.
Задание учебника 2023 года
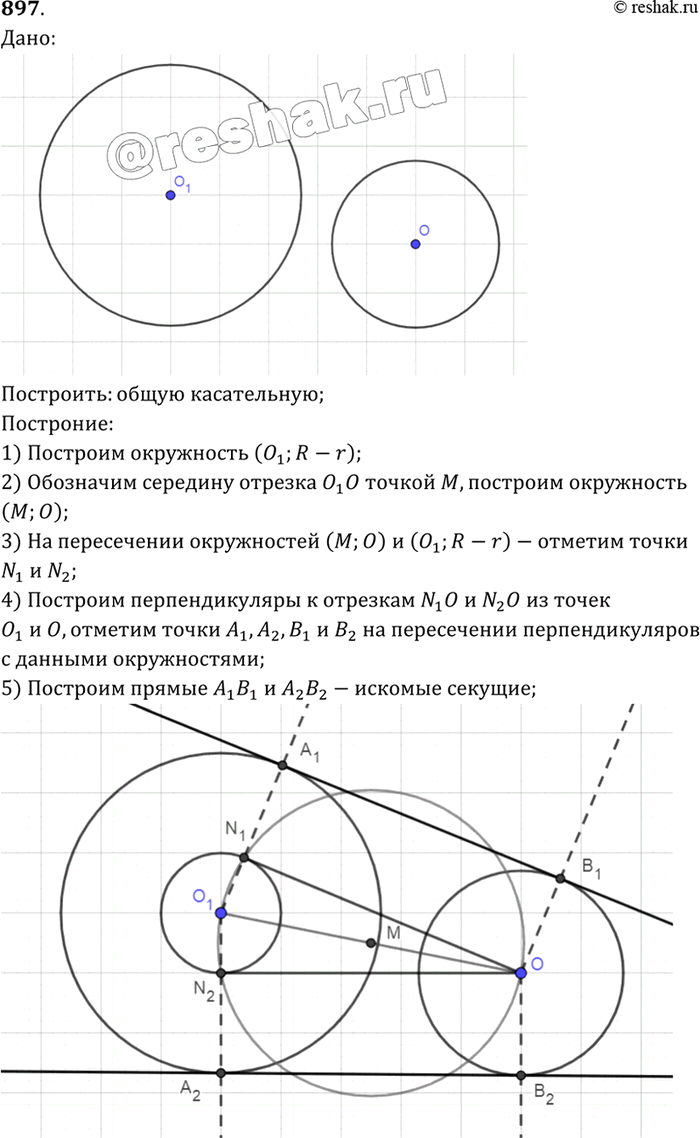
Постройте общую касательную к двум данным окружностям.
