Упр.782 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1(Учебник 2025)
Решение #2(Учебник 2023)
Рассмотрим вариант решения задания из учебника
Атанасян, Бутузов 7-9 класс, Просвещение:
Задание учебника 2025 года
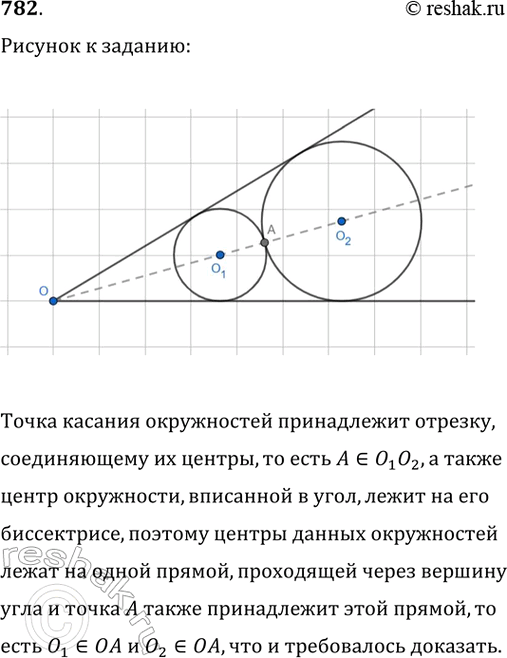
Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке А. Докажите, что центры этих окружностей лежат на прямой ОА.
Точка касания окружностей принадлежит отрезку, соединяющему их центры, то есть A принадлежит O_1 O_2,а также центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому центры данных окружностей лежат на одной прямой,проходящей через вершину угла и точка A также принадлежит этой прямой, то есть O_1 принадлежит OA и O_2 принадлежит OA,что и требовалось доказать.
Задание учебника 2023 года
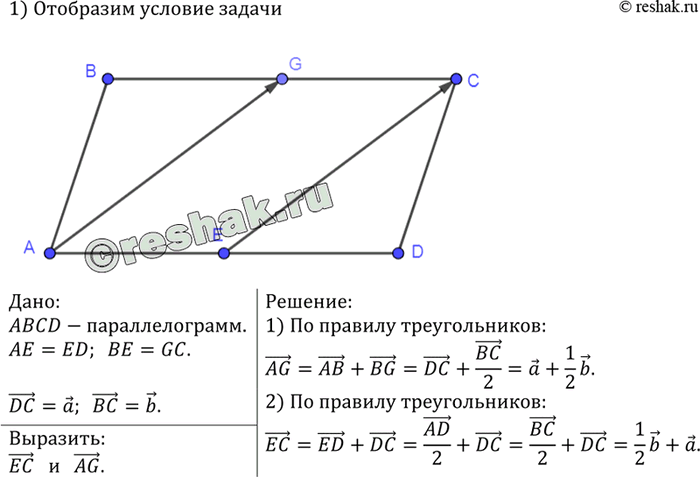
В параллелограмме ABCD точка Е — середина стороны AD, точка G — середина стороны ВС. Выразите векторы ЕС и AG через векторы DC = а и ВС = b.
