Упр.453 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)

Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
453. Даны две равные окружности с центрами O_1 и O_2, имеющие одну общую точку (такие окружности называются касающимися). Прямая m является касательной к каждой из них в точках А и В соответственно. Докажите, что отрезок АВ равен отрезку O_1O_2.
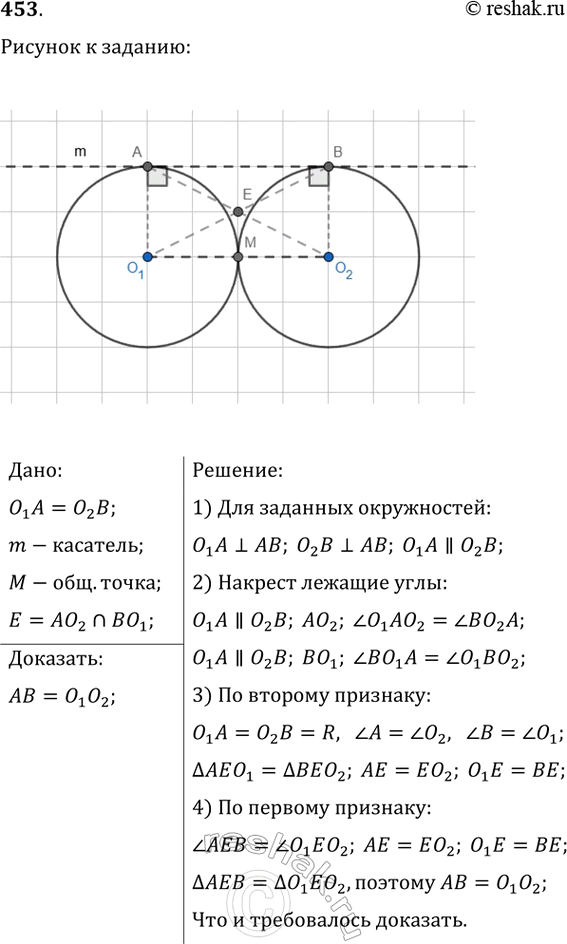
Дано:
O_1 A=O_2 B;
m-касатель;
M-общ.точка;
E=AO_2nBO_1;
Доказать:
AB=O_1 O_2;
Решение:
1) Для заданных окружностей:
O_1 A перпендикулярно AB; O_2 B перпендикулярно AB; O_1 A || O_2 B;
2) Накрест лежащие углы:
O_1 A || O_2 B; AO_2; угол O_1 AO_2=угол BO_2 A;
O_1 A || O_2 B; BO_1; угол BO_1 A=угол O_1 BO_2;
3) По второму признаку:
O_1 A=O_2 B=R, угол A=угол O_2, угол B=угол O_1;
треугольник AEO_1=треугольник BEO_2; AE=EO_2; O_1 E=BE;
4) По первому признаку:
угол AEB=угол O_1 EO_2; AE=EO_2; O_1 E=BE;
треугольник AEB=треугольник O_1 EO_2,поэтому AB=O_1 O_2;
Что и требовалось доказать.
Как изменится площадь прямоугольника, если: а) одну пару противоположных сторон увеличить в два раза; б) каждую сторону увеличить в два раза; в) одну пару противоположных сторон увеличить в два раза, а другую — уменьшить в два раза?
Похожие решебники
Популярные решебники 7 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







