Упр.831 ГДЗ Мерзляк Полонский 5 класс (Математика)
Решение #1(Учебник 2026)
Решение #2(Учебник 2019)
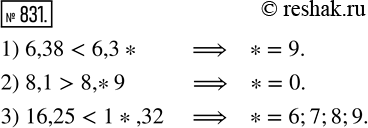
Решение #3(Учебник 2019)
Рассмотрим вариант решения задания из учебника
Мерзляк, Полонский, Якир 5 класс, Просвещение:
Задание учебника 2026 года
Запишите дробью, какая часть фигуры, изображённой на рисунке 190, закрашена.
Задание учебника 2019 года
Какие цифры можно поставить вместо звёздочки, чтобы образовалось верное неравенство:
1) 6,38 < 6,3*; 2) 8,1 > 8,*9; 3) 16,25 < 1*,32?
