Упр.828 ГДЗ Мерзляк Полонский 5 класс (Математика)
Решение #1 (Учебник 2024)
Решение #2 (Учебник 2024)
Решение #3 (Учебник 2019)
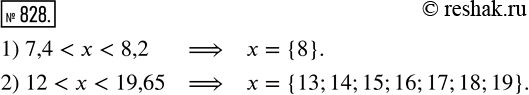
Решение #4 (Учебник 2019)
Рассмотрим вариант решения задания из учебника Мерзляк, Полонский, Якир 5 класс, Просвещение:
В записи первого трёхзначного числа используются только цифры 2 и 3, а в записи второго — только цифры 3 и 4. Может ли произведение этих чисел записываться только цифрами 2 и 4?
Рассмотрим наименьшее и наибольшее возможные произведения.
Чем меньше множители, тем меньше произведение.
222 – наименьшее число, которое можно составить из цифр 2 и 3.
333 – наименьшее число, которое можно составить из цифр 3 и 4.
222•333=73 926
Чем больше множители, тем больше произведение.
333 – наибольшее число, которое можно составить из цифр 2 и 3.
444 – наибольшее число, которое можно составить из цифр 3 и 4.
333•444=147 852
Все числа, состоящие только из цифр 2 и 3, находятся между числами 222 и 333.
Все числа, состоящие только из цифр 3 и 4, находятся между числами 333 и 444.
Поэтому, все возможные произведения находятся между числами 73 926 и 147 852.
Действительно, так как 222•333 - наименьшее произведение, то другие произведения не могут получиться меньше этого.
Аналогично, так как 333•444 - наибольшее произведение, то другие произведения не могут получиться больше этого.
Значит, на первом месте могут стоять только цифры 7, 8, 9 и 1, поэтому произведение не может состоять только из цифр 2 и 4.
Ответ: нет, не может.
Найдите все натуральные значения x, при которых верно неравенство:
1) 7,4 < х < 8,2; 2) 12 < x < 19,65.
Из двух десятичных дробей с неравными целыми частями больше та, у которой целая часть больше.
Если к десятичной дроби справа приписать любое количество нулей, то получится дробь, равная данной.
Для того, чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо:
1. с помощью приписывания нулей справа уравнять количество цифр в дробных частях;
2. сравнить полученные дроби поразрядно.
1) 7,4<x<8,2
8 – первое натуральное число, которое больше числа 7,4.
Действительно, 7<7,4, а 8>7,4.
7=7,0
У десятичных дробей 7,4 и 7,0 совпадают только целые части.
Необходимо сравнить десятые.
4>0, поэтому 7,4>7,0. Следовательно, 7,4>7.
8=8,0
У десятичных дробей 7,4 и 8,0 целые части неравны, сравним их.
7<8, поэтому 7,4<8,0. Следовательно, 7,4<8.
Все натуральные числа, которые больше 7, больше числа 7,4.
8 – последнее натуральное число, которое меньше числа 8,2.
Действительно, 8<8,2, а 9>8,2.
8=8,0
У десятичных дробей 8,0 и 8,2 совпадают только целые части.
Необходимо сравнить десятые.
0<2, поэтому 8,0<8,2. Следовательно, 8<8,2.
9=9,0
У десятичных дробей 9,0 и 8,2 целые части неравны, сравним их.
9>8, поэтому 9,0>8,2. Следовательно, 9>8,2.
Все натуральные числа, которые меньше 9, меньше числа 8,2.
Таким образом, подходят натуральные числа, которые больше 7 и меньше 9.
Подходит только число 8.
x=8.
2) 12<x<19,65
13 – первое натуральное число, которое больше числа 12.
19 – последнее натуральное число, которое меньше числа 19,65.
Действительно, 19<19,65, а 20>19,65.
19=19,00
У десятичных дробей 19,00 и 19,65 совпадают только целые части.
Необходимо сравнить десятые.
0<6, поэтому 19,00<19,65.
Следовательно, 19<19,65.
20=20,00
У десятичных дробей 20,0 и 19,65 целые части неравны, сравним их.
20>19, поэтому 20,00>19,65.
Следовательно, 20>19,65.
Все натуральные числа, которые меньше 20, меньше числа 19,65.
Таким образом, подходят натуральные числа, которые больше 12 и меньше 20.
x принимает значения 13, 14, 15, 16, 17, 18 и 19.
Похожие решебники
Популярные решебники 5 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением