Упр.5.53 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
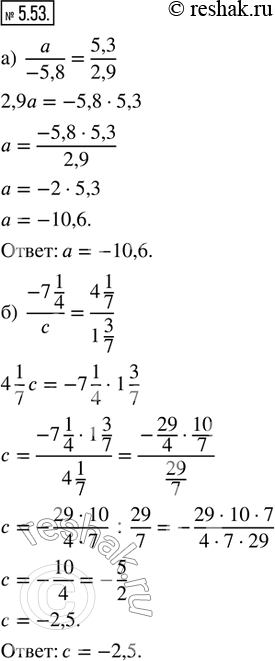
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
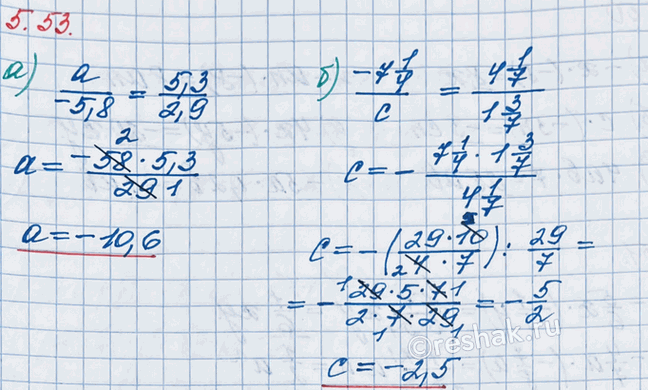
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите неизвестный член пропорции: а) а/-5,8 = 5,3/2,9; б) (-7 1/4)/c = (4 1/7)/(1 3/7).
а) Уравнение вида a/(-5,8)=5,3/2,9 представляет собой пропорцию.
Произведение крайних членов пропорции равно произведению её средних членов, тогда 2,9a=-5,8•5,3.
Откуда, выполнив умножение справа (для того, чтобы перемножить две десятичные дроби, необходимо умножить их как натуральные числа, не обращая внимание на запятые и в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе), получим уравнение 2,9a=-30,74, в котором неизвестен множитель a.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, тогда
a=-30,74:2,9
Для того, чтобы разделить десятичную дробь на десятичную, необходимо перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе; выполнить деление на натуральное число, не обращая внимание на запятую; поставить в частном запятую, когда кончится деление целой части, тогда a=-307,4:29
Или, a=-10,6.
б) Уравнение вида (-7 1/4)/c=(4 1/7)/(1 3/7) представляет собой пропорцию.
Произведение крайних членов пропорции равно произведению её средних членов, тогда 4 1/7•c=-7 1/4•1 3/7 .
В полученном уравнении неизвестен множитель c.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
c=-7 1/4•1 3/7 :4 1/7
Для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
c=-29/4•10/7 :29/7
Для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числа, стоящие в числителе и знаменателе, тогда c=-29/4•10/7•7/29
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей, значит, c=-(29•10•7)/(4•7•29)=-(2•5)/(2•2)=-5/2
Или, c=-5:2, так как черту дроби можно заменить делением.
Для того, чтобы выполнить деление, учитываем то, что любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой.
А для того, чтобы разделить десятичную дробь на натуральное число, необходимо дробь на это число, не обращая внимания на запятую; поставить в частном запятую, когда кончится деление целой части, тогда c=-2,5.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.