Упр.5.291 ГДЗ Виленкин Жохов 5 класс Часть 2, Просвещение (Математика)

Перейти к решению:#1(2025)#2(2025)#3(2025) ИИ

Решение #1(Учебник 2025)

Изображение Составьте уравнение, используя рисунок 47, и найдите его корни. а) По рисунку 142,а видно, что,...

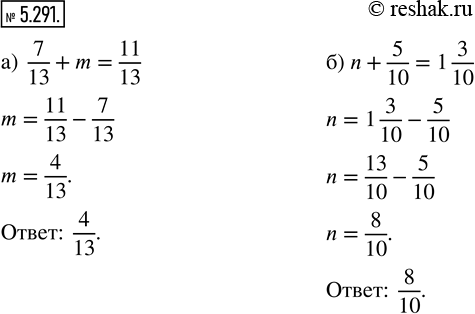
Решение #2(Учебник 2025)

Решение #3 (Учебник 2025)ИИ

Составить уравнения и найти корни
С пояснением а) 7/13 + m = 11/13.
Чтобы найти m, из конечной отметки вычтем первую:
m = 11/13 - 7/13 = 4/13.
б) n + 5/10 = 1 3/10.
1 3/10 = 13/10.
Чтобы найти n, вычтем 5/10:
n = 13/10 - 5/10 = 8/10 = 4/5.
Ответ: а) m = 4/13; б) n = 4/5.
Кратко а) 7/13 + m = 11/13,
m = 11/13 - 7/13 = 4/13.
б) n + 5/10 = 1 3/10,
n = 1 3/10 - 5/10 = 4/5.
Ответ: а) m = 4/13; б) n = 4/5.

Разбор подготовлен с помощью ИИ. Несмотря на проверку, возможны неточности.

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Александрова 5 класс, Просвещение:

Задание учебника 2025 года

Составьте уравнение, используя рисунок 47, и найдите его корни.

а) По рисунку 142,а видно, что, если к числу 7/13 прибавить m, получится 11/13 , то есть можно составить уравнение:

7/13+m=11/13

Неизвестно слагаемое m.

Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим:

m=11/13-7/13=(11-7)/13

Или, выполнив вычитание,

m=4/13

При выполнении вычитания опираемся на правило, согласно которому, чтобы найти разность двух дробей с одинаковыми знаменателями, необходимо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

б) По рисунку 142,б видно, что, если к числу n прибавить 5/10, получится 1 3/10 , то есть можно составить уравнение:

n+5/10=1 3/10

Неизвестно слагаемое n.

Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим:

n=1 3/10-5/10

n=(1+3/10)-5/10

n=(10/10+3/10)-5/10

n=(10+3)/10-5/10

n=13/10-5/10

n=(13-5)/10

n=8/10

При выполнении вычитания опираемся на правило, согласно которому, если дробная часть уменьшаемого меньше дробной части вычитаемого, то сначала преобразовываем уменьшаемое так, чтобы дробь в нём получилась неправильная, для этого:

представляем уменьшаемое в виде суммы целой части и дробной части;

в данном случае целую часть равна единице, которую представим в виде неправильной дроби, у которой числитель и знаменатель равны другу другу и равны знаменателю дробной части уменьшаемого;

полученную неправильную дробь складываем с дробной частью уменьшаемого;

выполняем вычитание дробей по правилу, согласно которому, чтобы найти разность двух дробей с одинаковыми знаменателями, необходимо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

*Текст задания приводится исключительно в образовательных целях для более полного понимания решения.