Упр.2.513 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
Решение #2 (Учебник 2023)

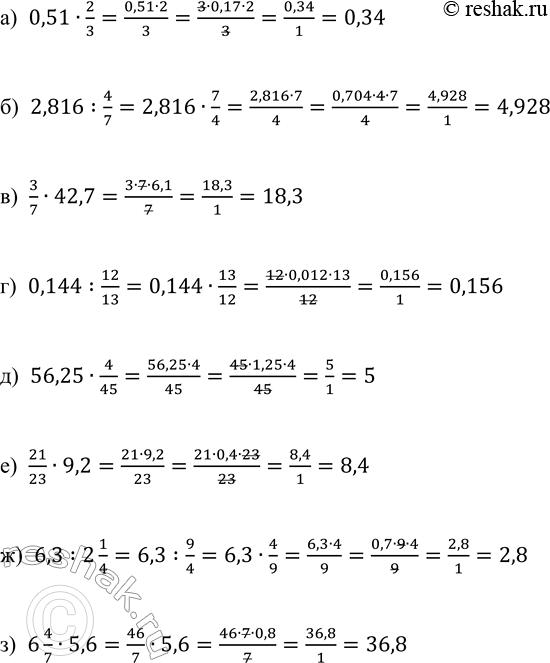
Решение #3 (Учебник 2023)
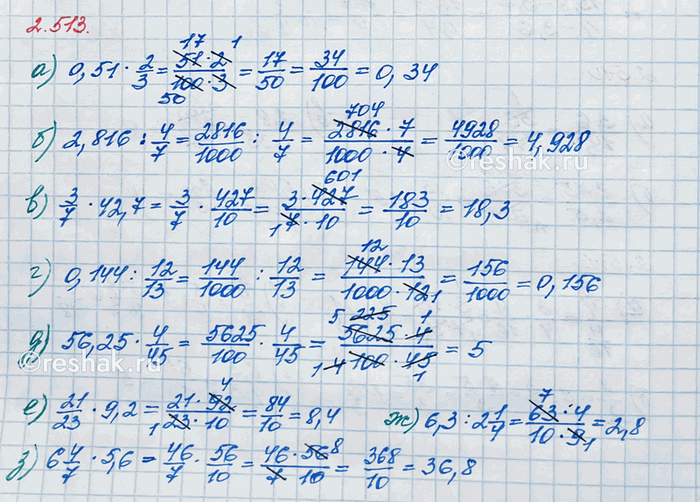
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
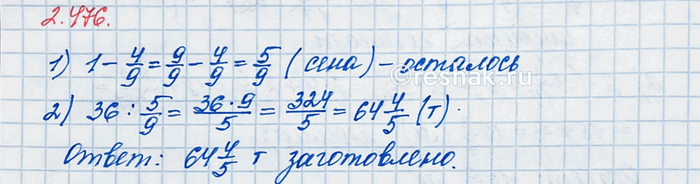
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действие:
а) 0,51 · 2/3; в) 3/7 · 42,7; д) 56,25 · 4/25; ж) 6,3 : 2 1/4;
б) 2,816 : 4/7; г) 0,144 : 12/13; е) 21/23 · 9,2; з) 6 4/7 · 5,6.
Для того, чтобы разделить две дроби, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель.
Произведением двух дробей является число, числитель которого равен произведению числителей, а знаменатель - произведению знаменателей.
Смешанные числа преобразовываем в неправильные дроби.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
При этом, прежде, чем перемножить числа, выполняем сокращение.
Для того, чтобы перемножить две десятичные дроби, необходимо умножить их как натуральные числа, не обращая внимание на запятые; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
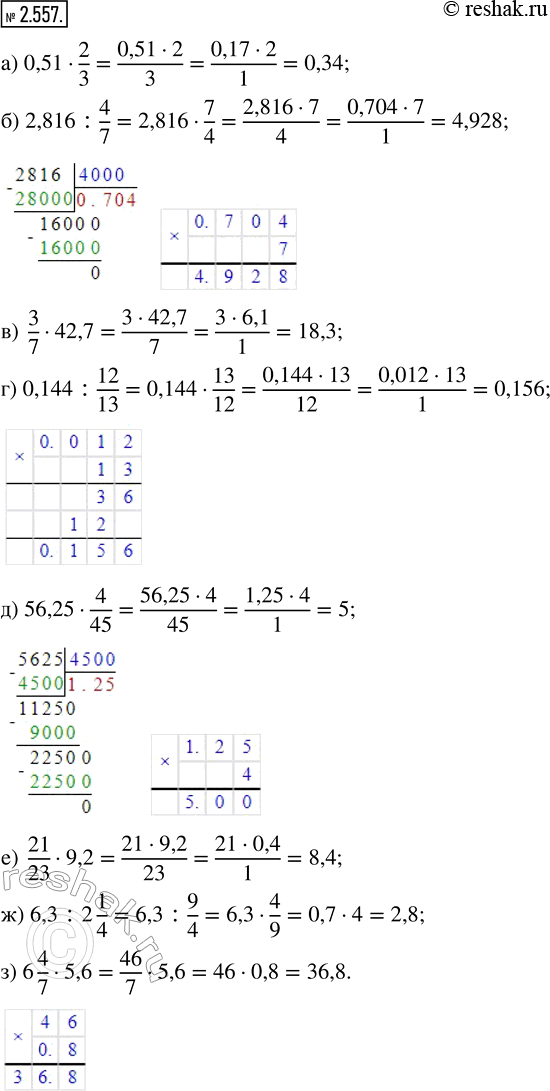
а) 0,51•2/3=(0,51•2)/3=(3•0,17•2)/3=0,34/1=0,34
б) 2,816:4/7=2,816•7/4=(2,816•7)/4=(0,704•4•7)/4=4,928/1=4,928
в) 3/7•42,7=(3•7•6,1)/7=18,3/1=18,3
г) 0,144:12/13=0,144•13/12=(12•0,012•13)/12=0,156/1=0,156
д) 56,25•4/45=(56,25•4)/45=(45•1,25•4)/45=5/1=5
е) 21/23•9,2=(21•9,2)/23=(21•0,4•23)/23=8,4/1=8,4
ж) 6,3:2 1/4=6,3:9/4=6,3•4/9=(6,3•4)/9=(0,7•9•4)/9=2,8/1=2,8
з) 6 4/7•5,6=46/7•5,6=(46•7•0,8)/7=36,8/1=36,8
После того как 4/9 заготовленного на зиму сена было израсходовано на кормление животных, осталось 36 т. Сколько тонн сена было заготовлено на зиму?
Всего было сена – 1.
Известно, что израсходовали 4/9 заготовленного на зиму сена.
Значит, 1-4/9=9/9-4/9=(9-4)/9=5/9 заготовленного сена осталось.
По условию задачи, осталось 36 т сена.
Для того, чтобы найти число по данному значению его дроби, необходимо это значение разделить на дробь.
Тогда, на зиму было заготовлено
36:5/9=36•9/5=(36•9)/5=324/5=64 4/5=64 (4•2)/(5•2)=64 8/10=64,8 т сена.
Для того, чтобы разделить натуральное число на обыкновенную дробь, необходимо делимое (натуральное число) умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель.
Для того, чтобы умножить натуральное число на дробь, необходимо числитель дроби умножить на это число и записать результат в числитель, а знаменатель оставить без изменений.
Если в результате вычислений получается неправильная дробь, числитель которой не делится нацело на знаменатель, то необходимо преобразовать её в смешанное число.
Для этого, необходимо числитель неправильной дроби разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, остаток от деления записать в числитель дробной части смешанного числа, а знаменатель оставить без изменений.
Ответ: 64,8 т.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









