Упр.2.516 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
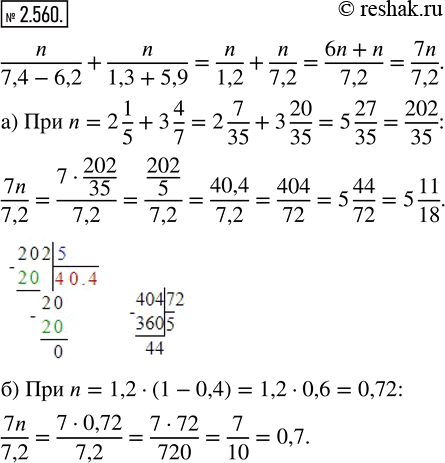
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
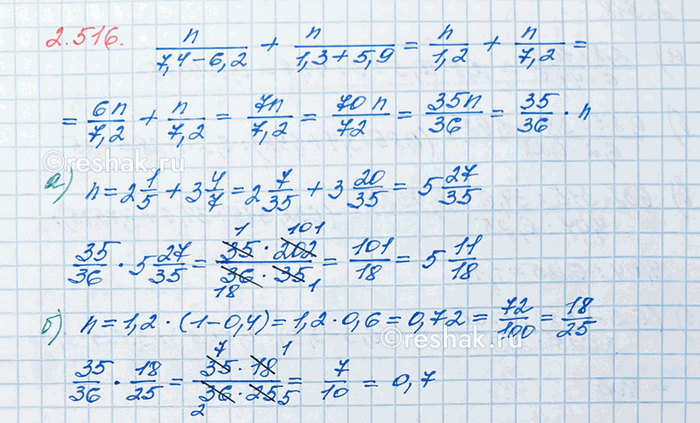
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите значение выражения n/(7,4-6,2) + n/(1,3+5,9) при:
а) n = 2 1/5 + 3 4/7; б) n = 1,2 · (1 - 0,4).
Если в числителе и знаменателе дробного выражения стоят десятичные дроби, то переносим в этих десятичных дробях запятые так, чтобы в числителе и знаменателе дробного выражения получились натуральные числа, причём количество знаков, на которые перенесли запятые в числителе дробного выражения, должно быть равно количеству знаков, на которые перенесли запятые в знаменателе дробного выражения.
В первую очередь преобразуем исходное выражение
n/(7,4-6,2)+n/(1,3+5,9)=n/1,2+n/7,2=(n•6)/(1,2•6)+n/7,2=6n/7,2+n/7,2=(6n+n)/7,2=7n/7,2
Основное свойство дроби – если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная данной.
При сложении (вычитании) дробей с равными знаменателями, числители дробей складывают (вычитают), а знаменатель оставляют без изменений.
а) При n=2 1/5+3 4/7=2 (1•7)/(5•7)+3 (4•5)/(7•5)=2 7/35+3 20/35=(2+3)+(7/35+20/35)=5+(7+20)/35=5 27/35=202/35
7n/7,2=(7•202/35)/7,2=((7•202)/35)/7,2=((7•202)/(5•7))/7,2=(202/5)/7,2=((202•2)/(5•2))/7,2=(404/10)/7,2=40,4/7,2=404/72=(4•101)/(4•18)=101/18=5 11/18
б) При n=1,2•(1-0,4)=1,2•0,6=0,72
7n/7,2=(7•0,72)/7,2=(7•72)/720=(7•72)/(72•10)=7/10=0,7
Как известно, Михаил Ломоносов отправился из Холмогор (Архангельская область) в Москву пешком. Первые три дня пути он шёл, догоняя обоз, который отправился из Холмогор на некоторое время раньше. Сколько километров прошёл М. Ломоносов, догоняя обоз, если в первый день он преодолел 10/29 всего пути, во второй день — 4/5 пути, пройденного в первый день, а в третий день — остальные 66 км?
Весь путь за три дня – это 1.
В первый день М. Ломоносов преодолел 10/29 всего пути.
Во второй день он преодолел 4/5 пути, пройденного во второй день, то есть
10/29•4/5=(10•4)/(29•5)=(2•5•4)/(29•5)=8/29 всего пути.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Значит, всего за два дня Ломоносов прошёл
10/29+8/29=(10+8)/29=18/29 всего пути.
Для того, чтобы сложить (вычесть) две дроби с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить без изменений.
Тогда, в третий день ему осталось пройти
1-18/29=29/29-18/29=(29-18)/29=11/29 всего пути.
Известно, что в третий день Ломоносов прошёл 66 км.
Для того, чтобы найти число по данному значению его дроби, необходимо это значение разделить на дробь.
Тогда, весь путь, который преодолел Ломоносов за три дня, составил 66:11/29=66•29/11=(66•29)/11=(6•11•29)/11=174/1=174 км.
Для того, чтобы разделить натуральное число на обыкновенную дробь, необходимо делимое (натуральное число) умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель.
Ответ: 174 км.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.