Упр.2.454 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1(Учебник 2026)
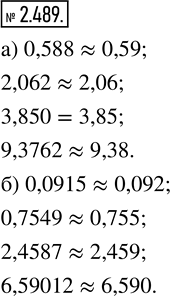
Решение #2(Учебник 2026)
Решение #3(Учебник 2026)
Решение #4 (Учебник 2026)ИИ
Округлите числа до сотых и тысячныхС пояснением
а) До сотых оставляем две цифры после запятой. Смотрим на третью цифру: если она 5 или больше, увеличиваем цифру сотых на 1.
0,588 ≈ 0,59;
2,062 ≈ 2,06;
3,850 ≈ 3,85;
9,3762 ≈ 9,38.б) До тысячных оставляем три цифры после запятой. Смотрим на четвёртую цифру:
0,0915 ≈ 0,092;
0,7549 ≈ 0,755;
2,4587 ≈ 2,459;
6,59012 ≈ 6,590.Ответ: а) 0,59; 2,06; 3,85; 9,38; б) 0,092; 0,755; 2,459; 6,590.
Кратко а) 0,588 ≈ 0,59; 2,062 ≈ 2,06; 3,850 ≈ 3,85; 9,3762 ≈ 9,38.
б) 0,0915 ≈ 0,092; 0,7549 ≈ 0,755; 2,4587 ≈ 2,459; 6,59012 ≈ 6,590.Ответ: а) 0,59; 2,06; 3,85; 9,38; б) 0,092; 0,755; 2,459; 6,590.
0,588 ≈ 0,59;
2,062 ≈ 2,06;
3,850 ≈ 3,85;
9,3762 ≈ 9,38.б) До тысячных оставляем три цифры после запятой. Смотрим на четвёртую цифру:
0,0915 ≈ 0,092;
0,7549 ≈ 0,755;
2,4587 ≈ 2,459;
6,59012 ≈ 6,590.Ответ: а) 0,59; 2,06; 3,85; 9,38; б) 0,092; 0,755; 2,459; 6,590.
Кратко а) 0,588 ≈ 0,59; 2,062 ≈ 2,06; 3,850 ≈ 3,85; 9,3762 ≈ 9,38.
б) 0,0915 ≈ 0,092; 0,7549 ≈ 0,755; 2,4587 ≈ 2,459; 6,59012 ≈ 6,590.Ответ: а) 0,59; 2,06; 3,85; 9,38; б) 0,092; 0,755; 2,459; 6,590.
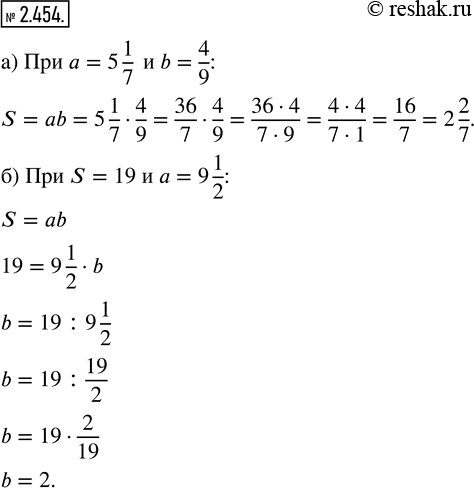
Решение #5(Учебник 2021)
Решение #6(Учебник 2021)
Решение #7(Учебник 2021)
Решение #8 (Учебник 2021)ИИ
Вычислить площадь и сторону прямоугольникаС пояснением
а) S = ab.
S = 5 1/7 · 4/9 = 36/7 · 4/9 = 16/7 = 2 2/7.б) Чтобы найти сторону b, площадь разделим на сторону a:
b = S : a.
b = 19 : 9 1/2 = 19 : 19/2 = 2.Ответ: а) 2 2/7; б) 2.
Кратко а) S = ab = 5 1/7 · 4/9 = 2 2/7.
б) b = S : a = 19 : 9 1/2 = 2.Ответ: а) 2 2/7; б) 2.
S = 5 1/7 · 4/9 = 36/7 · 4/9 = 16/7 = 2 2/7.б) Чтобы найти сторону b, площадь разделим на сторону a:
b = S : a.
b = 19 : 9 1/2 = 19 : 19/2 = 2.Ответ: а) 2 2/7; б) 2.
Кратко а) S = ab = 5 1/7 · 4/9 = 2 2/7.
б) b = S : a = 19 : 9 1/2 = 2.Ответ: а) 2 2/7; б) 2.
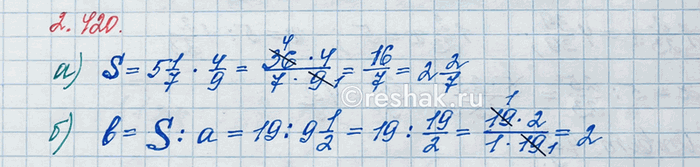
Рассмотрим вариант решения задания из учебника
Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Задание учебника 2026 года
Округлите числа:
а) 0,588; 2,062; 3,850; 9,3762 до сотых;
б) 0,0915; 0,7549; 2,4587; 6,59012 до тысячных.
Округление выполняем по следующему правилу:
- к цифре разряда, до которых округляют число прибавляют 1, если справа от неё стоят цифры 5, 6, 7, 8 или 9, а если справа от неё стоят цифры 0, 1, 2, 3 или 4, то цифру округляемого разряда оставляют без изменения.
- все цифры, расположенные правее разряда, до которого округляют число, отбрасывают.
а) До сотых:
0,588~0,59
2,062~2,06
3,850=3,85
9,3762~9,38
б) До тысячных:
0,0915~0,092
0,7549~0,755
2,4587~2,459
6,59012~6,590
Задание учебника 2021 года
Вычислите по формуле площади прямоугольника S = ab значение:
a) S при a = 5 1/7 и b = 4/9; б) b при S = 19 и a = 9 1/2.
Площадь прямоугольника вычисляется по формуле S=ab.
а) Если a=5 1/7 и b=4/9 , то, подставляя данные числовые значения, в формулу площади прямоугольника вместо букв, получим S=ab=5 1/7•4/9=36/7•4/9=(36•4)/(7•9)=(4•9•4)/(7•9)=16/7=2 2/7 .
Для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Для того, чтобы записать смешанное число в виде неправильной дроби, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
б) Если S=19 и a=9 1/2 , то, подставляя данные числовые значения, в формулу площади прямоугольника вместо букв, получим уравнение 19=9 1/2•b , в котором неизвестен множитель b.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
b=19:9 1/2
Далее преобразуем смешанное число 9 1/2 в неправильную дробь, для этого необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа, получим
b=19:19/2
Для того, чтобы разделить натуральное число на дробь, необходимо делимое (натуральное число) умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель, получим b=19•2/19 .
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения, получим b=(19•2)/19 , или, выполнив сокращение, b=(1•2)/1 или, выполнив умножение в числителе, b=2/1 или, учитывая то, что дробь, у которой в знаменателе стоит единица, равна числителю, b=2.
