Упр.2.450 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
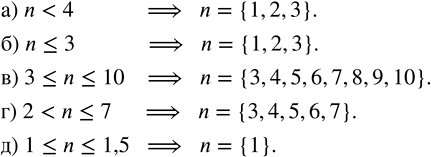
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
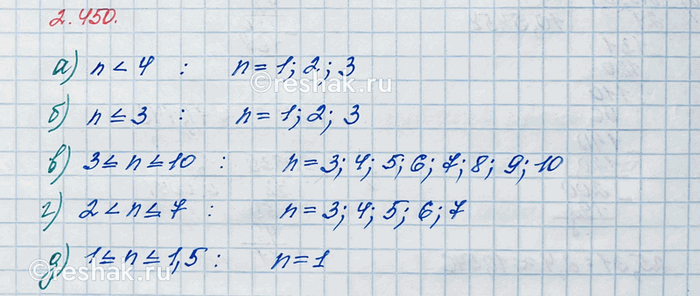
Решение #4 (Учебник 2021)
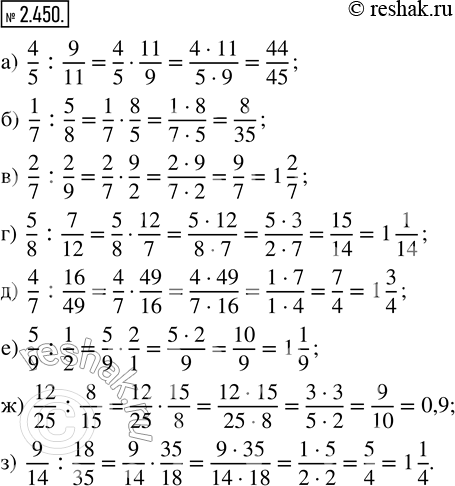
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Запишите множество натуральных чисел, которые являются решениями неравенства:
а) n < 4; 6) n ? 3; в) 3 ? n ? 10; г) 2 < n ? 7; д) 1 ? n ? 1,5.
Найдите частное:
а) 4/5 : 9/11; в) 2/7 : 2/9; д) 4/7 : 16/49; ж) 12/25 : 8/15;
б) 1/7 : 5/8; г) 5/8 : 7/12; е) 5/9 : 1/2; з) 9/14 : 18/35.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
- чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- при делении дроби на натуральное число, учитываем то, что любое натуральное число можно представить в виде дроби со знаменателем 1, затем пользуемся правилом деления дробей.
При этом, прежде, чем перемножить числа, выполняем сокращение.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
а) 4/5 :9/11=4/5•11/9=(4•11)/(5•9)=44/45
б) 1/7 :5/8=1/7•8/5=(1•8)/(7•5)=8/35
в) 2/7 :2/9=2/7•9/2=(2•9)/(7•2)=9/7=1 2/7
г) 5/8 :7/12=5/8•12/7=(5•12)/(8•7)=(5•3•4)/(2•4•7)=15/14=1 1/14
д) 4/7 :16/49=4/7•49/16=(4•49)/(7•16)=(4•7•7)/(7•4•4)=7/4=1 3/4
е) 5/9 :1/2=5/9•2=(5•2)/9=10/9=1 1/9
ж) 12/25 :8/15=12/25•15/8=(12•15)/(25•8)=(3•4•3•5)/(5•5•2•4)=9/10=0,9
з) 9/14 :18/35=9/14•35/18=(9•35)/(14•18)=(9•5•7)/(2•7•2•9)=5/4=1 1/4
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.