Упр.2.458 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)




Решение #3 (Учебник 2023)
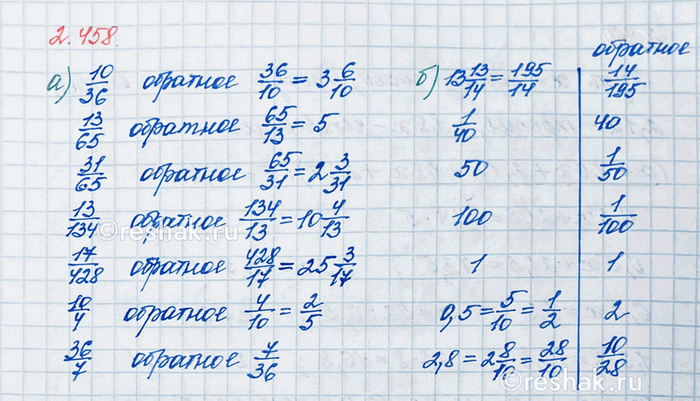
Решение #4 (Учебник 2021)
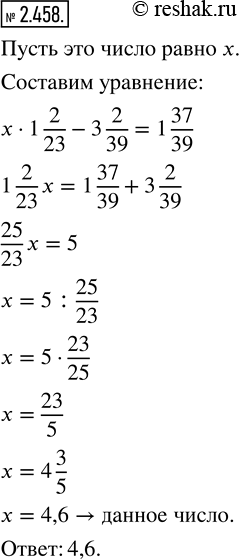
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Какие числа обратны числам:
а) 10/36, 13/65, 31/65, 13/134, 17/428, 10/4, 36/7;
б) 13 13/14; 1/40; 50; 100; 1; 0,5; 2,8?
Два числа, произведение которых равно 1, называют взаимно обратными.
Две обыкновенные дроби при умножении дают единицу, если числитель первой дроби равен знаменателю второй, а знаменатель первой равен числителю второй дроби.
Если обратная дробь получается неправильной (числитель больше знаменателя), то из неё нужно выделить целую часть, то есть представить в виде смешанного числа.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
Если необходимо найти число обратное смешанному числу, то это число нужно представить в виде неправильной дроби.
Для того, чтобы записать смешанное число в виде неправильной дроби, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
а) Числу 10/36 обратно число 36/10 , так как 10/36•36/10=(10•36)/(36•10)=1/1=1
При этом 36/10 - неправильная дробь, так как 36>10, значит, из неё можно выделить целую часть, то есть представить её в виде смешанного числа.
36:10=3 (ост.6), поэтому, 36/10=3 6/10=3,6 , поэтому числу 10/36 обратно число 3,6.
Числу 13/65 обратно число 65/13 , так как 13/65•65/13=(13•65)/(65•13)=1/1=1
При этом 65/13=5 , поэтому числу 13/65 обратно число 5.
Числу 31/65 обратно число 65/31 , так как 31/65•65/31=(31•65)/(65•31)=1/1=1
При этом 65/31 - неправильная дробь, так как 65>31, значит, из неё можно выделить целую часть, то есть представить её в виде смешанного числа.
65:31=2 (ост.3), поэтому, 65/31=2 3/31 , поэтому числу 31/65 обратно число 2 3/31 .
Числу 13/134 обратно число 134/13 , так как 13/134•134/13=(13•134)/(134•13)=1/1=1
При этом 134/13 - неправильная дробь, так как 134>13, значит, из неё можно выделить целую часть, то есть представить её в виде смешанного числа.
134:13=10 (ост.4), поэтому, 134/13=10 4/13 , поэтому числу 13/134 обратно число 10 4/13 .
Числу 17/428 обратно число 428/17 , так как 17/428•428/17=(17•428)/(428•17)=1/1=1
При этом 428/17 - неправильная дробь, так как 428>17, значит, из неё можно выделить целую часть, то есть представить её в виде смешанного числа.
428:17=25 (ост.3), поэтому, 428/17=25 3/17 , поэтому числу 17/128 обратно число 25 3/17 .
Числу 10/4 обратно число 4/10 , так как 10/4•4/10=(10•4)/(4•10)=1/1=1
Поэтому числу 10/4 обратно число 0,4.
Числу 36/7 обратно число 7/36 , так как 36/7•7/36=(36•7)/(7•36)=1/1=1
б) Число 13 13/14 - смешанное, чтобы найти число обратное ему, необходимо преобразовать его в неправильную дробь.
Получим 13•14+13=182+13=195, значит, 13 13/14=195/14 .
Тогда, числу 13 13/14 обратно число 14/195 , так как
13 13/14•14/195=195/14•14/195=(195•14)/(14•195)=1/1=1
Числу 1/40 обратно число 40/1 , так как 1/40•40/1=(1•40)/(40•1)=1/1=1
При этом 40/1=40 , поэтому числу 1/40 обратно число 40.
Числу 50 обратно число 1/50 , так как 50•1/50=(50•1)/50=1/1=1
При этом, 1/50=(1•2)/(50•2)=2/100=0,02.
Числу 100 обратно число 1/100 , так как 100•1/100=(100•1)/100=1/1=1
При этом, 1/100=0,01.
Числу 1 обратно число 1, так как 1•1/1=(1•1)/1=1/1=1.
То ест число 1 обратно самому себе.
Для того, чтобы найти число обратное десятичной дроби, необходимо эту дробь преобразовать в обыкновенную дробь, у которой в знаменателе стоит единица с нулями (количество нулей в знаменателе равно числу цифр после запятой в десятичной дроби).
Тогда, 0,5=5/10=(5•1)/(5•2)=1/2 .
Числу 1/2 обратно число 2 , так как 1/2•2=(1•2)/2=1/1=1
Значит, числу 2,5 обратно число 2.
Для того, чтобы найти число обратное десятичной дроби, необходимо эту дробь преобразовать в обыкновенную дробь, у которой в знаменателе стоит единица с нулями (количество нулей в знаменателе равно числу цифр после запятой в десятичной дроби).
Тогда, 2,8=2 8/10=2 (2•4)/(2•5)=2 4/5 .
Число 2 4/5 - смешанное, чтобы найти число обратное ему, необходимо преобразовать его в неправильную дробь.
Получим 2•5+4=10+4=14, значит, 2 4/5=14/5 .
Числу 14/5 обратно число 5/14 , так как 14/5•5/14=(14•5)/(5•14)=1/1=1
Значит, числу 2,8 обратно число 5/14 .
Некоторое число умножили на 1 2/23, от произведения отняли 3 2/39 и получили
1 37/39. Чему равно это число?
Решим задачу при помощи уравнения.
Пусть x – задуманное число.
Тогда, необходимо умножить x на 1 2/23 , затем из полученного произведения вычесть 3 2/39 , в результате получится 1 37/39 .
Следовательно, можем составить следующее уравнение:
x•1 2/23-3 2/39=1 37/39
1 2/23 x-3 2/39=1 37/39
Сначала решаем полученное уравнение относительно вычитания, то есть неизвестно уменьшаемое 1 2/23 x .
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
1 2/23 x=1 37/39+3 2/39
Для того, чтобы найти сумму двух смешанных чисел, необходимо отдельно сложить целые и дробные части чисел.
1 2/23 x=(1+3)+(37/39+2/39)
1 2/23 x=4+(37+2)/39
1 2/23 x=4+39/39
1 2/23 x=4+1
1 2/23 x=5
Далее решаем полученное уравнение относительно умножения, то есть неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=5:1 2/23
Для того, чтобы разделить натуральное число на смешанное число, необходимо сначала преобразовать смешанное число в неправильную дробь, тогда
x=5:25/23
Теперь необходимо делимое (натуральное число) умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель, получим
x=5•23/25
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения, значит
x=(5•23)/25
x=(5•23)/(5•5)
x=23/5
Дробь 23/5 – неправильная, так как 23>5.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать, как целую часть смешанного числа, а остаток – как числитель его дробной части, тогда
x=4 3/5 , так как 23:5=4 (ост.3)
x=4 3/5=4 (3•2)/(5•2)=4 6/10=4,6
Ответ: 4,6.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.