Упр.2.319 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
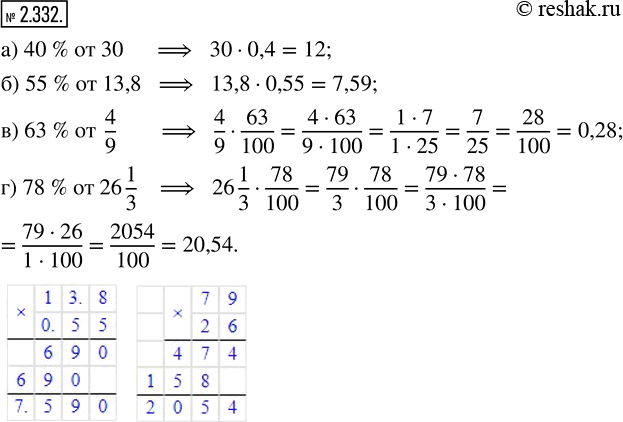
Решение #2 (Учебник 2023)
Решение #3 (Учебник 2023)
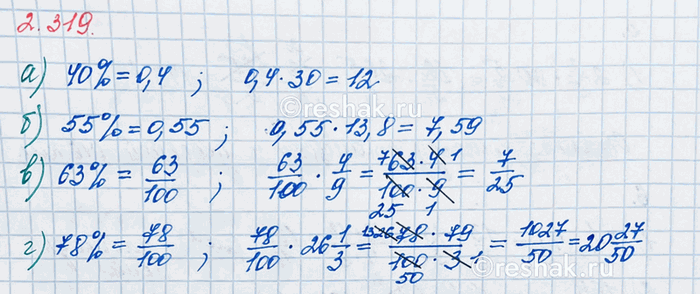
Решение #4 (Учебник 2021)
Решение #5 (Учебник 2021)
Решение #6 (Учебник 2021)
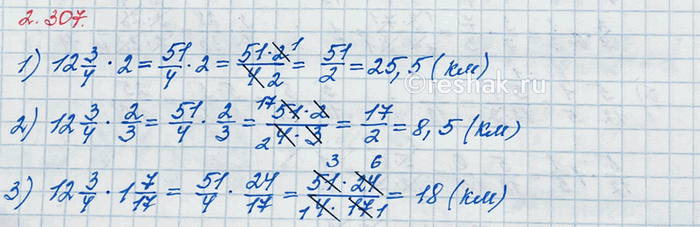
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Вычислите:
а) 40 % от 30; б) 55 % от 13,8; в) 63 % от 4/9; г) 78 % от 26 1/3.
Для того, чтобы найти часть от числа, выраженную в процентах, сначала необходимо перевести проценты в десятичную дробь, далее если нужно перевести десятичную дробь в обыкновенную и сократить её (если возможно), затем число умножить на полученную десятичную или обыкновенную дробь.
Для того, чтобы проценты перевести в десятичную дробь, необходимо число, стоящее перед знаком %, разделить на 100.
Для того, чтобы разделить десятичную дробь на 100, необходимо в этой дроби перенести запятую влево на две цифры.
Для того, чтобы десятичную дробь представить в виде обыкновенной, необходимо в знаменателе этой дроби получить единицу с нулями (число нулей равно числу цифр после запятой).
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Прежде чем перемножить обыкновенные дроби, выполняем сокращение дробей (если это возможно), то есть делим числитель и знаменатель на одно и то же число (наибольший общий делитель).
а) 40% от 30
40%=40:100=0,4
30•0,4=12
б) 55% от 13,8
55%=55:100=0,55
13,8•0,55=7,59
в) 63% от 4/9
63%=63:100=0,63
0,63=63/100
4/9•63/100=(4•63)/(9•100)=(4•7•9)/(9•4•25)=7/25=(7•4)/(25•4)=28/100=0,28
г) 78% от 26 1/3
78%=78:100=0,78
0,78=78/100=(2•39)/(2•50)=39/50
26 1/3•39/50=79/3•39/50=(79•39)/(3•50)=(79•3•13)/(3•50)=1027/50=(1027•2)/(50•2)=2054/100=20,54
Велосипедист едет со скоростью 12 3/4 км/ч. Какое расстояние он проедет за 2 ч, 2/3 ч и 1 7/17 ч?
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы выполнить умножение смешанных чисел, необходимо представить их в виде неправильных дробей.
- для того, чтобы найти произведение дроби и натурального числа, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
- при умножении необходимо выполнять сокращение, если это возможно, для удобства расчётов. Для этого необходимо одно из чисел числителя и знаменателя разделить на одно и то же число и далее выполнять умножение.
Для того, чтобы найти расстояние (пройденный путь), необходимо скорость движения умножить на время в пути.
Двигаясь со скоростью 12 3/4 км/ч за 2 часа велосипедист проедет
12 3/4•2=51/4•2=(51•2)/4=(51•2)/(2•2)=51/2=25 1/2=25,5 (км).
Двигаясь со скоростью 12 3/4 км/ч за 2/3 часа велосипедист проедет
12 3/4•2/3=51/4•2/3=(51•2)/(4•3)=(3•17•2)/(2•2•3)=17/2=8 1/2=8,5 (км).
Двигаясь со скоростью 12 3/4 км/ч за 1 7/17 часа велосипедист проедет
12 3/4•1 7/17=51/4•24/17=(51•24)/(4•17)=(3•17•4•6)/(4•17)=18/1=18 (км).
Ответ: 25,5 км; 8,5 км; 18 км.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением