Упр.2.320 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1(Учебник 2026)
Решение #2(Учебник 2026)
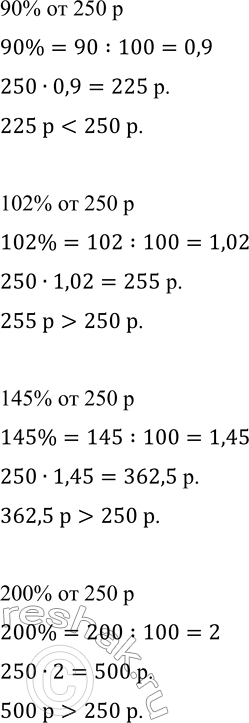
Решение #3(Учебник 2026)
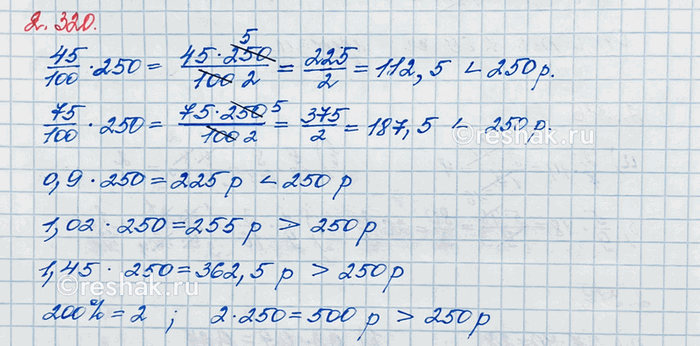
Решение #4(Учебник 2021)
Решение #5(Учебник 2021)
Решение #6(Учебник 2021)
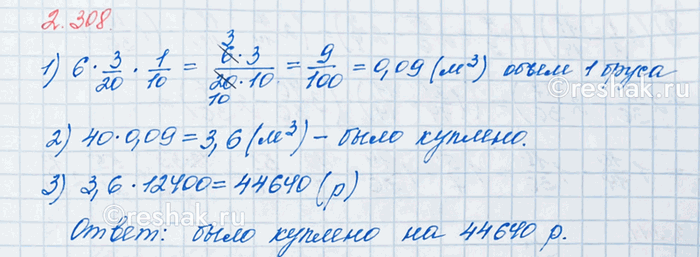
Рассмотрим вариант решения задания из учебника
Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Задание учебника 2026 года
Андрей решил 1 1/5 задач от 30 запланированных задач для решения на неделю. Сколько задач он решил?
Задание учебника 2021 года
Деревянный брус имеет форму прямоугольного параллелепипеда, измерения которого равны 6 м, 3/20 м и 1/10 м. Для выполнения строительных работ было куплено 40 штук такого бруса по цене 6400 р. за 1 м^3. На какую сумму был закуплен брусугол При выполнении вычислений опираемся на следующие правила:
- для того, чтобы найти произведение дроби и натурального числа, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
- при умножении необходимо выполнять сокращение, если это возможно, для удобства расчётов. Для этого необходимо одно из чисел числителя и знаменателя разделить на одно и то же число и далее выполнять умножение.
Найдём объём деревянного бруса, который имеет форму прямоугольного параллелепипеда.
Объём прямоугольного параллелепипеда равен произведению трёх его измерений - длины, ширины и высоты.
Значит, объём бруса равен
6•3/20•1/10=(6•3•1)/(20•10)=(2•3•3)/(2•10•10)=9/100=0,09 (м^3) – объём деревянного бруса.
Было куплено 40 таких брусьев, значит, их объём составил
40•0,09=3,6 (м^3) – общий объём брусьев.
Для того, чтобы найти сумму закупа всего бруса, необходимо стоимость 1 м^3 бруса умножить на общий объём брусьев.
Известно, что цена 1 м^3 бруса 6400 р.
6400•3,6=23040 (р) – сумма закупа бруса.
Ответ: 23 040 рублей.
