Упр.2.208 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
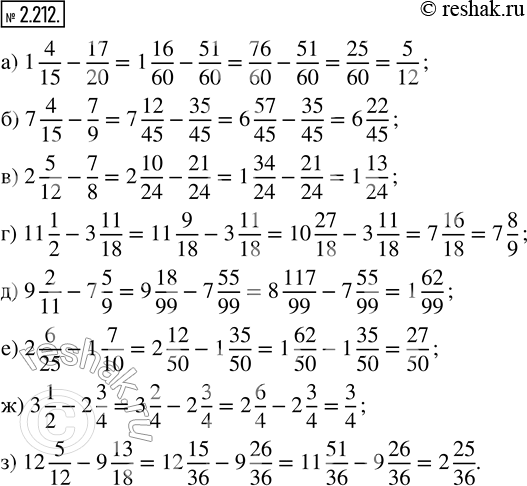
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
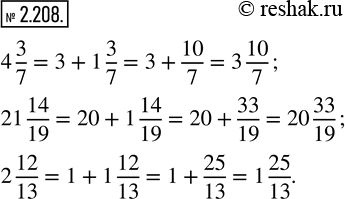
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действие:
а) 1 4/15 - 17/20; в) 2 5/12 - 7/8; д) 9 2/11 - 7 5/9; ж) 3 1/2 - 2 3/4;
б) 7 4/15 - 7/9; г) 11 1/2 - 3 11/18; е) 2 6/25 - 1 7/10; з) 12 5/12 - 9 13/18.
Для того, чтобы выполнить вычитание смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить вычитание целых частей и дробных частей.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь равная данной.
Если в первом числителе стоит число меньше, чем во втором числителе, то необходимо занять единицу у целой части и представить её в виде неправильной дроби совместно с данной дробью, затем отдельно выполнить вычитание целых частей и дробных частей.
Если в ответе получается сократимая дробь, необходимо числитель и знаменатель разделить на одно и то же число.
а) 1 4/15-17/20=1 (4•4)/(15•4)-(17•3)/(20•3)=1 16/60-51/60=(1+16/60)-51/60=(60/60+16/60)-51/60=(60+16)/60-51/60=76/60-51/60=(76-51)/60=25/60=(5•5)/(5•12)=5/12
б) 7 4/15-7/9=7 (4•3)/(15•3)-(7•5)/(9•5)=7 12/45-35/45=(6+1+12/45)-35/45=(6+45/45+12/45)-35/45=(6+(45+12)/45)-35/45=(6+57/45)-35/45=(6-0)+(57/45-35/45)=6+(57-35)/45=6 22/45
в) 2 5/12-7/8=2 (5•2)/(12•2)-(7•3)/(8•3)=2 10/24-21/24=(1+1+10/24)-21/24=(1+24/24+10/24)-21/24=(1+(24+10)/24)-21/24=(1+34/24)-21/24=(1-0)+(34/24-21/24)=1+(34-21)/24=1 13/24
г) 11 1/2-3 11/18=11 (1•9)/(2•9)-3 11/18=11 9/18-3 11/18=(10+1+9/18)-(3+11/18)=(10+18/18+9/18)-(3+11/18)=(10+(18+9)/18)-(3+11/18)=(10+27/18)-(3+11/18)=(10-3)+(27/18-11/18)=7+(27-11)/18=7 16/18=7 (2•8)/(2•9)=7 8/9
д) 9 2/11-7 5/9=9 (2•9)/(11•9)-7 (5•11)/(9•11)=9 18/99-7 55/99=(8+1+18/99)-(7+55/99)=(8+99/99+18/99)-(7+55/99)=(8+(99+18)/99)-(7+55/99)=(8+117/99)-(7+55/99)=(8-7)+(117/99-55/99)=1+(117-55)/99=1 62/99
е) 2 6/25-1 7/10=2 (6•2)/(25•2)-1 (7•5)/(10•5)=2 12/50-1 35/50=(1+1+12/50)-(1+35/50)=(1+50/50+12/50)-(1+35/50)=(1+(50+12)/50)-(1+35/50)=(1-1)+(62/50-35/50)=(62-35)/50=27/50
ж) 3 1/2-2 3/4=3 (1•2)/(2•2)-2 3/4=3 2/4-2 3/4=(2+1+2/4)-(2+3/4)=(2+4/4+2/4)-(2+3/4)=(2+(4+2)/4)-(2+3/4)=(2-2)+(6/4-3/4)=0+(6-3)/4=3/4
з) 12 5/12-9 13/18=12 (5•3)/(12•3)-9 (13•2)/(18•2)=12 15/36-9 26/36=(11+1+15/36)-(9+26/36)=(11+36/36+15/36)-(9+26/36)=(11+51/36)-(9+26/36)=(11-9)+(51/36-26/36)=2+(51-26)/36=2 25/36
Уменьшив целую часть на 1, запишите в виде неправильной дроби дробную часть чисел 4 3/7, 21 14/19, 2 12/13.
Запись числа 4 3/7 содержит целую (4) и дробную (3/7) части.
4 3/7=4+3/7.
Представим целую часть (4) в виде суммы (3+1).
Запишем натуральное число 1 в виде дроби с натуральным знаменателем 7.
1=7/7
Тогда, число 4 3/7 запишем так, что целая часть будет равна 3, а дробная 7/7+3/7.
Вычислим дробную часть: 7/7+3/7=(7+3)/7=10/7.
Таким образом, смешанное число 4 3/7 можно записать в виде 3 10/7
Запись числа 21 14/19 содержит целую (21) и дробную (14/19) части.
21 14/19=21+14/19.
Представим целую часть (21) в виде суммы (20+1).
Запишем натуральное число 1 в виде дроби с натуральным знаменателем 19.
1=19/19
Тогда, число 21 14/19 запишем так, что целая часть будет равна 20, а дробная 19/19+14/19.
Вычислим дробную часть: 19/19+14/19=(19+14)/19=33/19.
Таким образом, смешанное число 21 14/19 можно записать в виде 20 33/19.
Запись числа 2 12/13 содержит целую (2) и дробную (12/13) части.
2 12/13=2+12/13.
Представим целую часть (2) в виде суммы (1+1).
Запишем натуральное число 1 в виде дроби с натуральным знаменателем 13.
1=13/13
Тогда, число 2 12/13 запишем так, что целая часть будет равна 1, а дробная 13/13+12/13.
Вычислим дробную часть: 13/13+12/13=(13+12)/13=25/13.
Таким образом, смешанное число 2 12/13 можно записать в виде 1 25/13.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









