Упр.669 ГДЗ Макарычев Миндюк 9 класс (Алгебра)

Решение #1 (Учебник 2026)

Изображение 669 Пусть (un) — последовательность чисел Фибоначчи, т. е. u1 = 1, u2 = 1, un+2 = un + un+1 при n > 2. Докажите,...

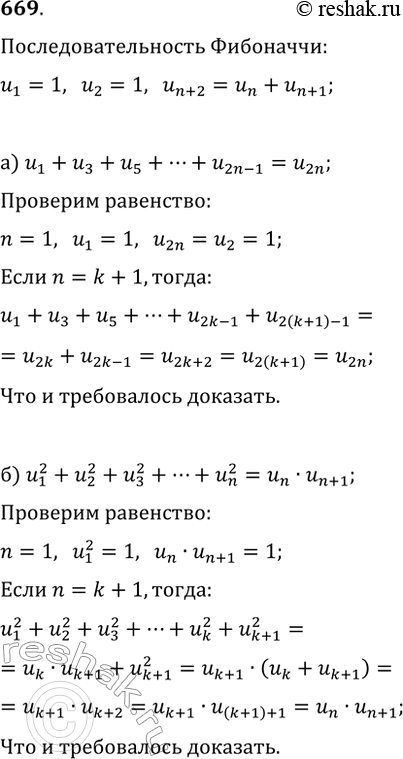
Решение #2 (Учебник 2024)

Решение #3 (Учебник 2024)

Рассмотрим вариант решения задания из учебника Макарычев, Миндюк, Нешков 9 класс, Просвещение:

Задание учебника 2026 года

Последовательность (x_n) — геометрическая прогрессия. Является ли геометрической прогрессией последовательность:

а) x_1 + 1; x_2 + 1; ...; x_n + 1; ...;

б) 3x_1; 3x_2; ...; 3x_n; ...;

в) x_1^2; x_2^2; ...; x_n^2; ...;

г) 1/x_1; 1/x_2; ...; 1/x_n; ...?

Задание учебника 2024 года

Пусть (un) — последовательность чисел Фибоначчи, т. е. u1 = 1, u2 = 1, un+2 = un + un+1 при n > 2. Докажите, что эта последовательность обладает следующим свойством:

а) u1 + u3 + u5 + ... + u2n-1 = u2n;

б) u 2/1 + u 2/2 + u2/3 + ... + u 2/n = un * un+1.

*Текст задания приводится исключительно в образовательных целях для более полного понимания решения.