Упр.7.29 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 8 класс, Просвещение:
29. Известно, что диагонали четырёхугольника пересекаются. Докажите, что сумма их длин меньше периметра, но больше полупериметра четырёхугольника.
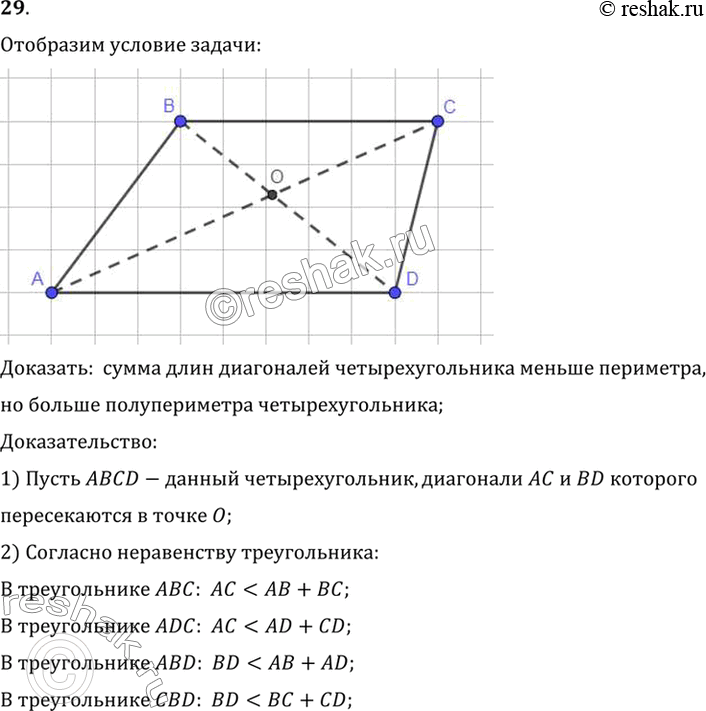
Доказать: сумма длин диагоналей четырехугольника меньше периметра,
но больше полупериметра четырехугольника;
Доказательство:
1) Пусть ABCD-данный четырехугольник, диагонали AC и BD которого
пересекаются в точке O;
2) Согласно неравенству треугольника:
В треугольнике ABC: AC
В треугольнике ADC: AC
В треугольнике ABD: BD
В треугольнике CBD: BD
3) Сложим все четыре эти неравенства между собой, получим:
2(AC+BD)<2(AB+BC+CD+AD), отсюда AC+BD
4) Согласно неравенству треугольника:
В треугольнике AOB: AB
В треугольнике BOC: BC
В треугольнике COD: CD
В треугольнике DOA: AD
5) Сложим все четыре эти неравенства между собой, получим:
AB+BC+CD+AD<2(OA+OC)+2(OB+OD), отсюда P<2(AC+BD);
6) Разделим обе части выражения на 2, получим: AC+BD>P/2;
7) Таким образом: P/2
Популярные решебники 8 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением