Упр.692 ГДЗ Макарычев Миндюк 9 класс (Углубленный) (Алгебра)
Решение #1
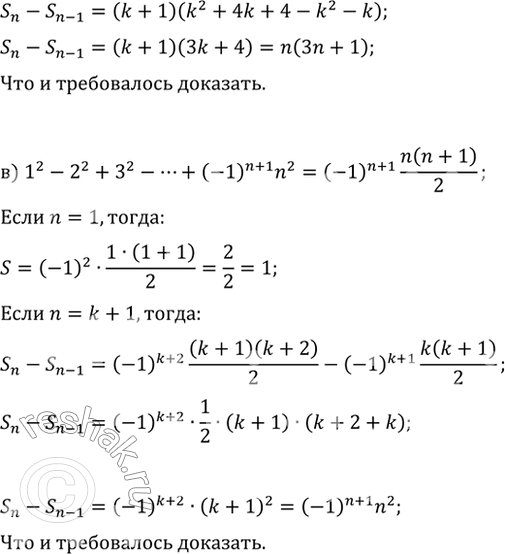
Рассмотрим вариант решения задания из учебника Макарычев, Миндюк, Нешков 9 класс, Просвещение:
692. Докажите, что при любом натуральном n:
а) 1·2+2·3+3·4+...+n(n+1)=n(n+1)(2n+1)/3;
б) 1·4+2·7+3·10+...+n(3n+1)=n(n+1)^2;
в) 1^2-2^2+3^2-4^2+...+(-1)^(n+1) n^2=(-1)^(n+1) n(n+1)/2.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
