Упр.2.67 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
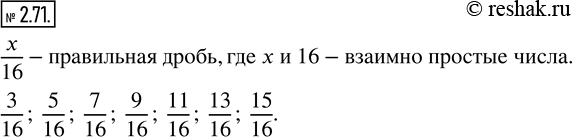
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
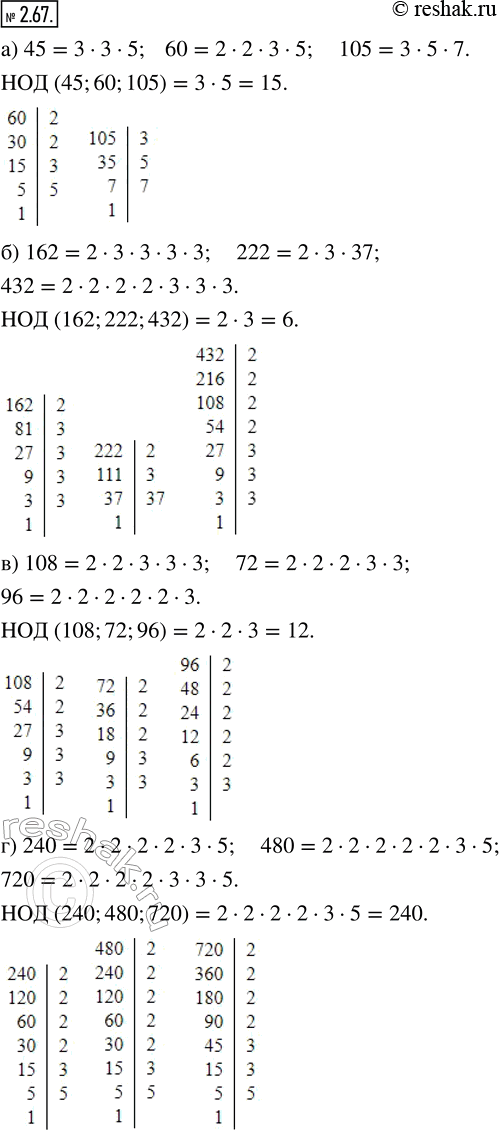
Решение #5 (Учебник 2021)



Решение #6 (Учебник 2021)
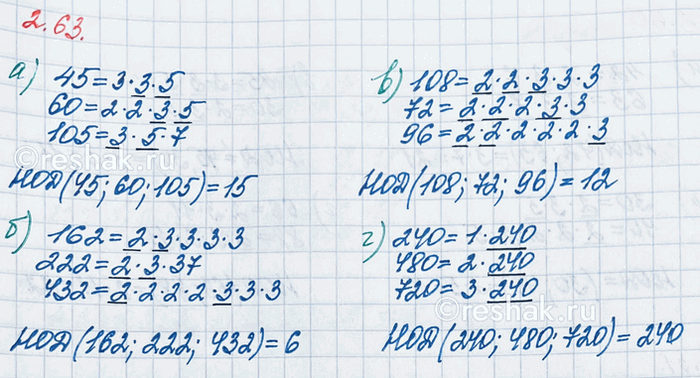
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите все правильные дроби, знаменатель которых равен 16, а числитель и знаменатель — взаимно простые числа.
Правильные дроби со знаменателем 16:
1/16,2/16,3/16,…,14/16,15/16
(числитель меньше знаменателя).
Из этих дробей необходимо выбрать такие, у которых числитель (число над чертой) и знаменатель (число под чертой) являются взаимно простыми числами (их наибольший общий делитель равен 1).
НОД (1;16)=1
НОД (2;16)=2
НОД (3; 16)=1
И так далее.
Числа в знаменателе и в числителе не вызывают затруднений для устного перебора всех дальнейших пар.
Приходим к выводу, что
НОД (1;16)=1
НОД (3;16)=1
НОД (5;16)=1
НОД (7;16)=1
НОД (9;16)=1
НОД (11;16)=1
НОД (13;16)=1
НОД (15;16)=1
Так как общих делителей, кроме 1, у чисел 1 и 16; 3 и 16; 5 и 16; 7 и 16; 9 и 16; 11 и 16; 13 и 16; 15 и 16 нет.
Найдите наибольший общий делитель чисел:
а) 45, 60 и 105; в) 108, 72 и 96:
б) 162, 222 и 432; г) 240, 480 и 720.
а) Разложим числа 45, 60 и 105 на простые множители и подчеркнём общие множители чисел.
45=3•3•5
60=2•2•3•5
105=3•5•7
Общие множители чисел: 3; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (45;60;105)=3•5=15
б) Разложим числа 162, 222 и 432 на простые множители и подчеркнём общие множители чисел.
162=2•3•3•3•3
222=2•3•37
432=2•2•2•2•3•3•3
Общие множители чисел: 2; 3.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (162;222;432)=2•3=6
в) Разложим числа 108, 72 и 96 на простые множители и подчеркнём общие множители чисел.
108=2•2•3•3•3
72=2•2•2•3•3
96=2•2•2•2•2•3
Общие множители чисел: 2; 2; 3.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (108;72;96)=2•2•3=4•3=12
г) Разложим числа 240, 480 и 720 на простые множители и подчеркнём общие множители чисел.
240=2•2•2•2•3•5
480=2•2•2•2•2•3•5
720=2•2•2•2•3•3•5
Общие множители чисел: 2; 2; 2; 2; 3; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (240;480;720)=2•2•2•2•3•5=10•24=240
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









