Упр.2.422 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
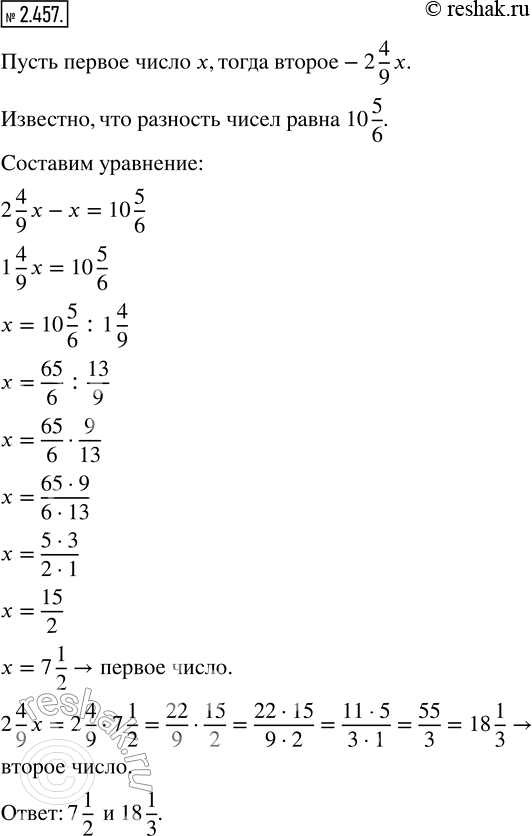
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
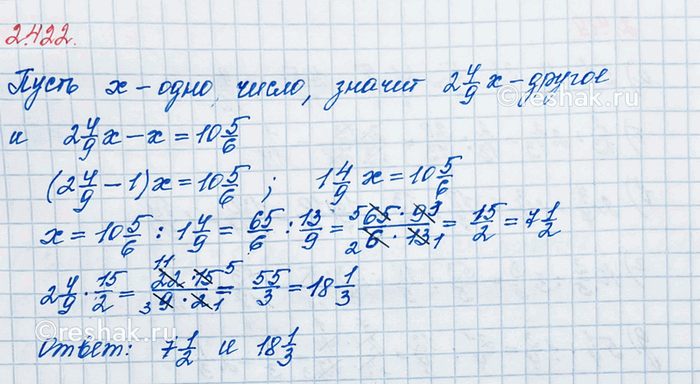
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
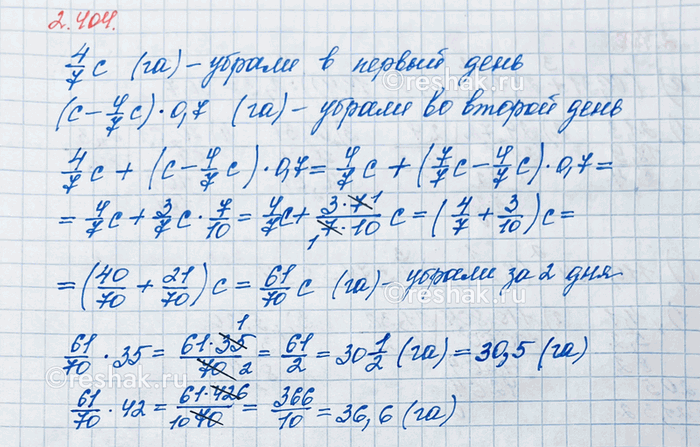
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Одно число в 2 4/9 раза больше другого. Найдите эти числа, если их разность равна 10 5/6.
Решим задачу при помощи уравнения.
Пусть x – первое число.
Тогда, второе число 2 4/9 x, так как одно число в 2 4/9 раза больше другого.
При этом разность этих двух чисел равна 10 5/6 .
Следовательно, можем составить следующее уравнение:
2 4/9 x-x=10 5/6
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число,
2 4/9 x-1•x=10 5/6
Далее используем распределительное свойство умножения относительно вычитания, то есть выносим одинаковый множитель x за скобки, получим
(2 4/9-1)x=10 5/6
Или, выполнив вычитание в скобках,
1 4/9 x=10 5/6
Далее решаем уравнение относительно умножения, то есть неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=10 5/6 :1 4/9
Для того, чтобы выполнить деление смешанных чисел, их необходимо перевести в неправильные дроби.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части, тогда
x=65/6 :13/9
x=65/6•9/13
x=(65•9)/(6•13)
x=(5•13•3•3)/(2•3•13)
x=15/2
x=7 1/2
Для того, чтобы разделить одну обыкновенную дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
При этом, прежде, чем перемножить числа, выполняем сокращение.
Значит, первое число равно 7 1/2 .
Второе число равно
2 4/9 x=2 4/9•7 1/2=22/9•15/2=(22•15)/(9•2)=(2•11•3•5)/(3•3•2)=55/3=18 1/3
Ответ: 7 1/2; 18 1/3 .
В первый день убрали 4/7 площади, засеянной подсолнечником, во второй день - 0,7 оставшейся площади. Сколько гектаров подсолнечника убрали за эти два дня, если было засеяно с га? Найдите значение получившегося выражения при с = 35; с = 42.
Для того, чтобы найти дробь от числа, необходимо дробь умножить на данное число.
По условию в первый день убрали 4/7 от всей площади, засеянной подсолнечником, то есть 4/7 c (га) – убрали в первый день.
Для того, чтобы найти площадь, оставшуюся после первого дня, необходимо из общей засеянной площади вычесть площадь, которую убрали в первый день, то есть после первого дня осталось c-4/7 c=7/7 c-4/7 c=(7/7-4/7)c=(7-4)/7 c=3/7 c (га).
По условию, во второй день убрали 0,7 оставшейся площади.
Для того, чтобы найти площадь, убранную во второй день, необходимо 0,7 умножить на оставшуюся после первого дня площадь, получим, что во второй день убрали
0,7•3/7 c=7/10•3/7 c=(7•3)/(10•7) c=3/10 c (га) – площади.
Для того, чтобы найти, какую площадь убрали за 2 дня, необходимо сложить площади, убранные в первый и во второй дни, то есть за два дня убрали
4/7 c+3/10 c=(4/7+3/10)c=((4•10)/(7•10)+(3•7)/(10•7))c=(40/70+21/70)c=(40+21)/70 c=
=61/70 c (га) – подсолнечника убрали за эти два дня.
При c=35, 61/70 c=61/70•35=(61•35)/70=(61•35)/(35•2)=61/2=30 1/2=30 (1•5)/(2•5)=
=30 5/10=30,5 (га) – подсолнечника убрали за 2 дня.
При c=42, 61/70 c=61/70•42=(61•42)/70=(61•14•3)/(14•5)=183/5=36 3/5=36 (3•2)/(5•2)=36 6/10=36,6 (га) – подсолнечника убрали за 2 дня.
Ответ: 61/70 c га; 30,5 га; 36,6 га.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









