Упр.2.428 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
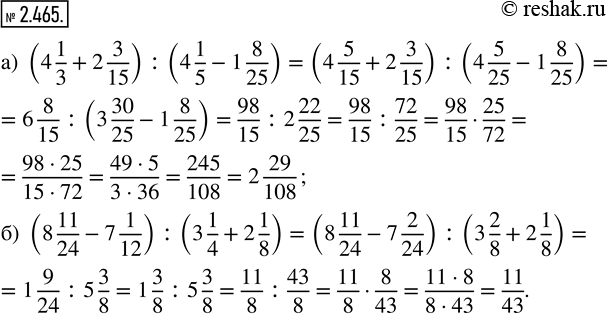
Решение #2 (Учебник 2023)

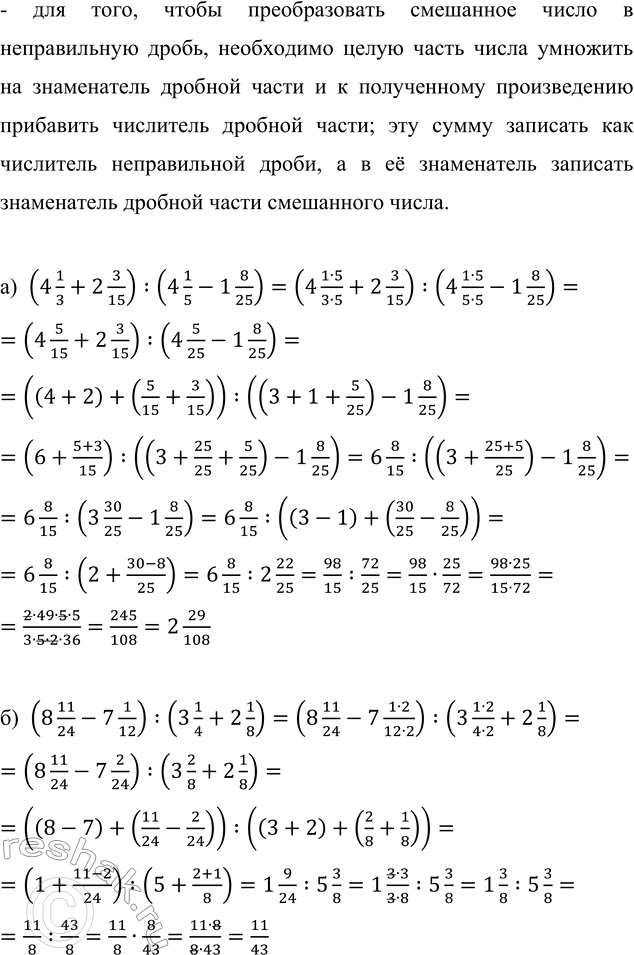
Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
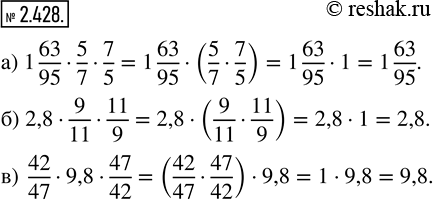
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
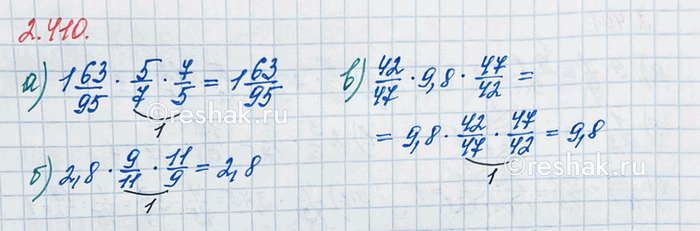
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действия:
а) (4 1/3 + 2 3/15) : (4 1/5 - 1 8/25); б) (8 11/24 - 7 1/12) : (3 1/4 + 2 1/8).
При вычислениях опираемся на следующие правила:
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение (деление) смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения (деления) дробей.
При этом, прежде, чем перемножить числа, выполняем сокращение.
- для того, чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
- для того, чтобы сложить (вычесть) дроби с разными знаменателями, необходимо привести данные дроби к наименьшему общему знаменателю, а затем сложить (вычесть) полученные дроби.
- для того, чтобы сложить (вычесть) смешанные числа, необходимо отдельно сложить (вычесть) их целые и дробные части.
- для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать, как целую часть смешанного числа, а остаток – как числитель его дробной части.
- для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
а) (4 1/3+2 3/15) :(4 1/5-1 8/25)=(4 (1•5)/(3•5)+2 3/15) :(4 (1•5)/(5•5)-1 8/25)=(4 5/15+2 3/15) :(4 5/25-1 8/25)=((4+2)+(5/15+3/15)) :((3+1+5/25)-1 8/25)=(6+(5+3)/15) :((3+25/25+5/25)-1 8/25)=6 8/15 :((3+(25+5)/25)-1 8/25)=6 8/15 :(3 30/25-1 8/25)=6 8/15 :((3-1)+(30/25-8/25))=6 8/15 :(2+(30-8)/25)=6 8/15 :2 22/25=98/15 :72/25=98/15•25/72=(98•25)/(15•72)=(2•49•5•5)/(3•5•2•36)=245/108=2 29/108
б) (8 11/24-7 1/12) :(3 1/4+2 1/8)=(8 11/24-7 (1•2)/(12•2)) :(3 (1•2)/(4•2)+2 1/8)=(8 11/24-7 2/24) :(3 2/8+2 1/8)=((8-7)+(11/24-2/24)) :((3+2)+(2/8+1/8))=(1+(11-2)/24) :(5+(2+1)/8)=1 9/24 :5 3/8=1 (3•3)/(3•8) :5 3/8=1 3/8 :5 3/8=11/8 :43/8=11/8•8/43=(11•8)/(8•43)=11/43
Вычислите произведение:
а) 1 63/95 · 5/7 · 7/5; б) 2,8 · 9/11 · 11/9; в) 42/47 · 9,8 · 47/42.
При выполнении вычислений используем сочетательное свойство умножения, то есть сначала перемножаем взаимно обратные числа, которые при умножении дают единицу, затем умножаем на единицу оставшийся множитель и в ответе получаем этот множитель, так как при умножении единицы на любое число, получим равное ему число.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
а) 1 63/95•5/7•7/5=1 63/95•(5/7•7/5)=1 63/95•(5•7)/(7•5)=1 63/95•1/1=1 63/95•1=1 63/95
б) 2,8•9/11•11/9=2,8•(9/11•11/9)=2,8•(9•11)/(11•9)=2,8•1/1=2,8•1=2,8
в) 42/47•9,8•47/42=(42/47•47/42)•9,8=(42•47)/(47•42)•9,8=1/1•9,8=1•9,8=9,8
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.