Упр.2.313 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
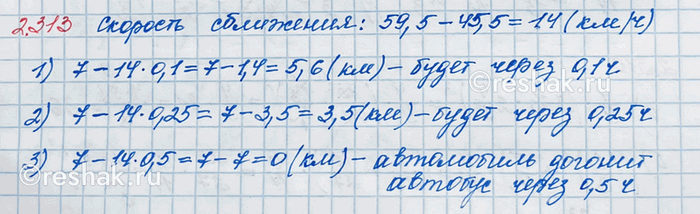
Решение #4 (Учебник 2021)
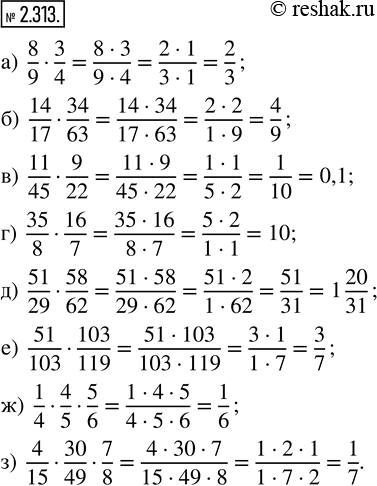
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
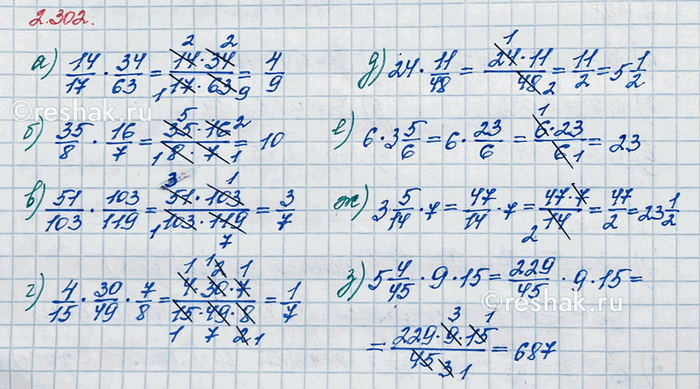
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Автомобиль догоняет автобус. Сейчас расстояние между ними 7 км. Скорость автобуса 45,5 км/ч, а скорость автомобиля 59,5 км/ч. Какое расстояние будет между ними через t ч, если t = 0,1; t = 0,25; t = 0,5?
Автомобиль догоняет автобус, то есть автомобиль и автобус сближаются.
Скорость автобуса 45,5 км/ч, а скорость автомобиля 59,5 км/ч.
Тогда, учитывая то, что автобус и автомобиль двигаются в одном направлении, скорость сближения автобуса и автомобиля будет равна 59,5-45,5=14 (км/ч).
Для того, чтобы найти расстояние, необходимо скорость умножить на время в пути.
Скорость сближения автомобиля и автобуса 14 км/ч, значит, за время t ч расстояние между автомобилем и автобусом изменится на 14t (км).
При этом, изначально расстояние между автомобилем и автобусом было 7 км, значит, через t часов расстояние между ними станет равным 7-14t (км).
Далее, чтобы найти расстояние между автомобилем и автобусом через время t=0,1;0,25;0,5 ч, необходимо в буквенное выражение 7-14t вместо t подставить соответствующие числа и выполнить вычисления, сначала умножение, а затем вычитание, получим что:
если t=0,1 ч, то 7-14t=7-14•0,1=7-1,4=5,6 (км)
если t=0,25 ч, то 7-14t=7-14•0,25=7-3,5=3,5 (км)
если t=0,5 ч, то 7-14t=7-14•0,5=7-7=0 (км), то есть через 0,5 ч автомобиль догонит автобус.
Для того, чтобы умножить десятичную дробь на натуральное число, необходимо умножить их как натуральные числа, не обращая внимания на запятую; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой у умножаемой дроби.
Найдите произведение:
а) 8/9 · 3/4; в) 11/45 · 9/22; д) 51/29 · 58/62; ж) 1/4 · 4/5 · 5/6;
б) 14/17 · 34/63; г) 35/8 · 16/7; е) 51/103 · 103/119; з) 4/15 · 30/49 · 7/8.
Для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
При умножении необходимо выполнять сокращение, если это возможно, для удобства расчётов. Для этого необходимо одно из чисел числителя и знаменателя разделить на одно и то же число и далее выполнять умножение.
а) 8/9•3/4=(8•3)/(9•4)=(2•4•3)/(3•3•4)=2/3
б) 14/17•34/63=(14•34)/(17•63)=(7•2•17•2)/(17•7•9)=4/9
в) 11/45•9/22=(11•9)/(45•22)=(11•9)/(9•5•2•11)=1/10=0,1
г) 35/8•16/7=(35•16)/(8•7)=(5•7•2•8)/(8•7)=10/1=10
д) 51/29•58/62=(51•58)/(29•62)=(51•2•29)/(29•2•31)=51/31=1 20/31
е) 51/103•103/119=(51•103)/(103•119)=(3•17•103)/(103•7•17)=3/7
ж) 1/4•4/5•5/6=(1•4•5)/(4•5•6)=1/6
з) 4/15•30/49•7/8=(4•30•7)/(15•49•8)=(4•2•15•7)/(15•7•7•4•2)=1/7
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









