Упр.2.197 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
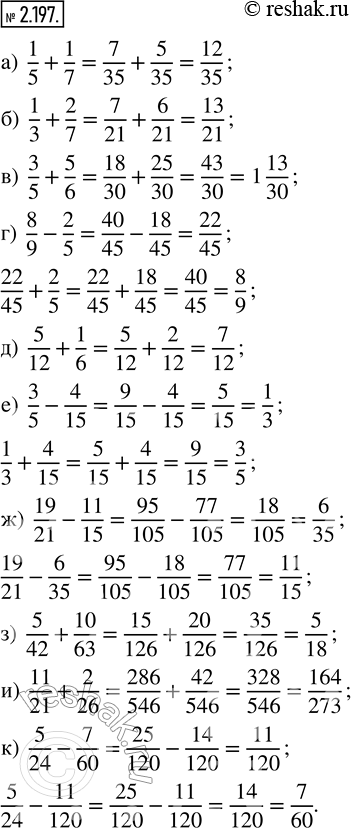
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Лена полола первую грядку 1/3 ч, вторую на 1/5 ч меньше, а третью на 2/15 ч больше, чем первую и вторую вместе. Сколько времени ушло у Лены на прополку?
Для того, чтобы определить, сколько времени Лена полола две грядки, необходимо сложить время на прополку первой грядки со временем на прополку второй грядки.
На вторую грядку у Лены ушло меньше времени, чем на первую.
Значит, найдём время на прополку второй грядки, с помощью вычитания.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают (вычитают), а знаменатель оставляют тот же.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
1/3-1/5=(1•5)/(3•5)-(1•3)/(5•3)=5/15-3/15=(5-3)/15=2/15 (ч) – Лена полола вторую грядку.
Теперь определим, сколько времени Лена потратила на прополку двух грядок.
1/3+2/15=(1•5)/(3•5)+2/15=5/15+2/15=(5+2)/15=7/15 (ч) – Лена полола две грядки.
Известно, что третью грядку Лена полола дольше (больше), чем две первые грядки вместе.
Значит, найдём время на третью грядку с помощью сложения.
7/15+2/15=(7+2)/15=9/15 (ч) – полола Лена третью грядку.
Наконец найдём, сколько времени ушло у Лены на прополку трёх грядок.
Для этого сложим время, потраченное на первые две грядки, и время, потраченное на третью грядку.
7/15+9/15=(7+9)/15=16/15=1 1/15 (ч) – ушло у Лены на прополку.
Ответ: 1 1/15 часа.
Выполните действие:
а) 1/5 + 1/7; в) 3/5 + 5/6; д) 5/12 + 1/6; ж) 19/21 - 11/15; и) 11/21 + 2/26;
б) 1/3 + 2/7; г) 8/9 - 2/5; е) 3/5 - 4/15; з) 5/42 + 10/63; к) 5/24 - 7/60.
В примерах г) и е) выполненное вычитание проверьте сложением, в примерах ж) и к) — вычитанием.
Для того, чтобы сложить (вычесть) дроби с одинаковыми знаменателями, необходимо сложить (вычесть) числители, а знаменатель оставить прежним.
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.
а) 1/5+1/7=(1•7)/(5•7)+(1•5)/(7•5)=7/35+5/35=(7+5)/35=12/35
б) 1/3+2/7=(1•7)/(3•7)+(2•3)/(7•3)=7/21+6/21=(7+6)/21=13/21
в) 3/5+5/6=(3•6)/(5•6)+(5•5)/(6•5)=18/30+25/30=(18+25)/30=43/30=1 13/30
г) 8/9-2/5=(8•5)/(9•5)-(2•9)/(5•9)=40/45-18/45=(40-18)/45=22/45
Проверка – уменьшаемое должно быть равно сумме вычитаемого и разности.
2/5+22/45=(2•9)/(5•9)+22/45=18/45+22/45=(18+22)/45=40/45=(5•8)/(5•9)=8/9 – верно.
д) 5/12+1/6=5/12+(1•2)/(6•2)=5/12+2/12=(5+2)/12=7/12
е) 3/5-4/15=(3•3)/(5•3)-4/15=9/15-4/15=(9-4)/15=5/15=(5•1)/(3•5)=1/3
Проверка – уменьшаемое должно быть равно сумме вычитаемого и разности.
4/15+1/3=4/15+(1•5)/(3•5)=4/15+5/15=(4+5)/15=9/15=(3•3)/(3•5)=3/5 – верно.
ж) 19/21-11/15=(19•5)/(21•5)-(11•7)/(15•7)=95/105-77/105=(95-77)/105=18/105=(3•6)/(3•35)=6/35
Проверка – вычитаемое должно быть равно разности уменьшаемого и разности.
19/21-6/35=(19•5)/(21•5)-(6•3)/(35•3)=95/105-18/105=(95-18)/105=77/105=(7•11)/(7•15)=11/15 – верно.
з) 5/42+10/63=(5•3)/(42•3)+(10•2)/(63•2)=15/126+20/126=(15+20)/126=35/126=(5•7)/(7•18)=5/18
и) 11/21+2/26=(11•26)/(21•26)+(2•21)/(26•21)=286/546+42/546=(286+42)/546=328/546=(2•164)/(2•273)=164/273
к) 5/24-7/60=(5•5)/(24•5)-(7•2)/(60•2)=25/120-14/120=(25-14)/120=11/120
Проверка – вычитаемое должно быть равно разности уменьшаемого и разности.
5/24-11/120=(5•5)/(24•5)-11/120=25/120-11/120=(25-11)/120=14/120=(2•7)/(2•60)=7/60 – верно.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









