Упр.2.176 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
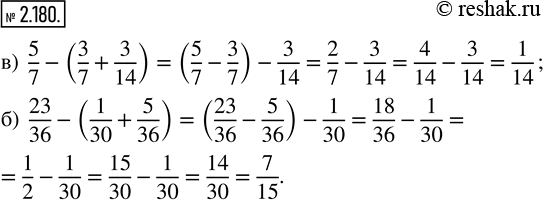
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
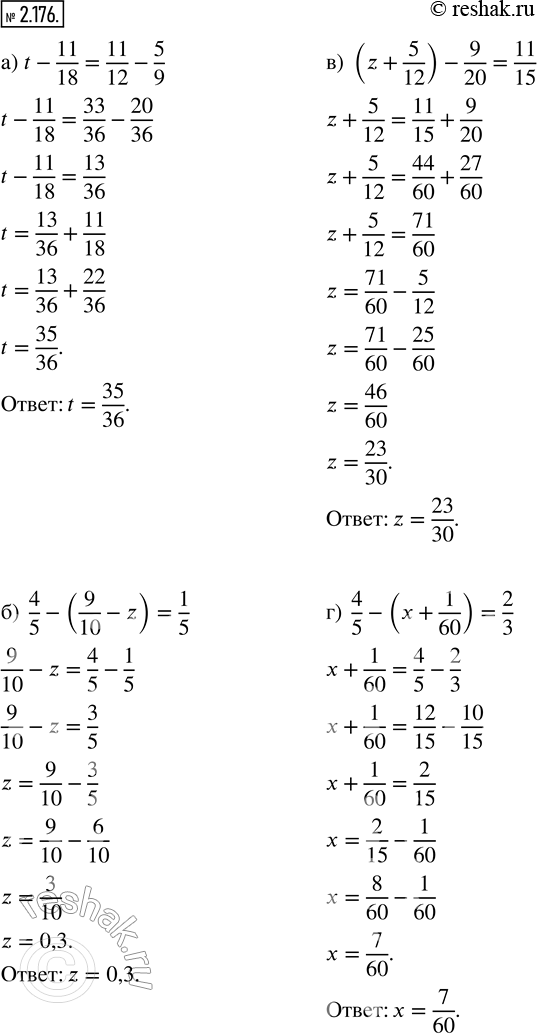
Решение #5 (Учебник 2021)



Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
С помощью свойства вычитания суммы из числа вычислите значение выражения:
а) 5/7 - (3/7 + 3/14); б) 23/36 - (1/30 + 5/36).
При сложении (вычитании) дробей с одинаковыми знаменателями, числители складывают (вычитают), а знаменатель оставляют тот же.
а) Для того, чтобы вычесть сумму 3/7+3/14 из дроби 5/7 , можно сначала вычесть из 5/7 слагаемое 3/7 с таким же знаменателем (7), и из полученной разности затем вычесть другое слагаемое 3/14 .
5/7-(3/7+3/14)=(5/7-3/7)-3/14=(5-3)/7-3/14=2/7-3/14
Приведём дроби к общему знаменателю 14.
2/7-3/14=(2•2)/(7•2)-3/14=4/14-3/14=(4-3)/14=1/14
б) Для того, чтобы вычесть сумму 1/30+5/36 из дроби 23/36 , можно сначала вычесть из 23/36 слагаемое 5/36 с таким же знаменателем (36), и из полученной разности затем вычесть другое слагаемое 1/30 .
23/36-(1/30+5/36)=(23/36-5/36)-1/30=(23-5)/36-1/30=18/36-1/30
Сократим первую дробь на 18.
18/36-1/30=(18•1)/(18•2)-1/30=1/2-1/30
Приведём дроби к общему знаменателю 30.
1/2-1/30=(1•15)/(2•15)-1/30=15/30-1/30=(15-1)/30=14/30
Сократим дробь на 2.
14/30=(2•7)/(2•15)=7/15
Решите уравнение:
а) t - 11/18 = 11/12 - 5/9; в) (z + 5/12) - 9/20 = 11/15;
б) 4/5 - (9/10 - z) = 1/5; г) 4/5 - (x + 1/60) = 2/3.
Для того, чтобы сложить (вычесть) дроби с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.
а) t-11/18=11/12-5/9
Выполним вычитание в правой части выражения.
t-11/18=(11•3)/(12•3)-(5•4)/(9•4)
t-11/18=33/36-20/36
t-11/18=(33-20)/36
t-11/18=13/36
В уравнении неизвестно уменьшаемое t.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
t=13/36+11/18
t=13/36+(11•2)/(18•2)
t=13/36+22/36
t=(13+22)/36
t=35/36
б) 4/5-(9/10-z)=1/5
В уравнении неизвестно вычитаемое 9/10-z.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
9/10-z=4/5-1/5
9/10-z=(4-1)/5
9/10-z=3/5
В уравнении вновь неизвестно вычитаемое z, получим
z=9/10-3/5
z=9/10-(3•2)/(5•2)
z=9/10-6/10
z=(9-6)/10
z=3/10=0,3
в) (z+5/12)-9/20=11/15
В уравнении неизвестно уменьшаемое z+5/12.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
z+5/12=11/15+9/20
z+5/12=(11•4)/(15•4)+(9•3)/(20•3)
z+5/12=44/60+27/60
z+5/12=(44+27)/60
z+5/12=71/60
В уравнении неизвестно слагаемое z.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
z=71/60-5/12
z=71/60-(5•5)/(12•5)
z=71/60-25/60
z=(71-25)/60
z=46/60=(2•23)/(2•30)=23/30
г) 4/5-(x+1/60)=2/3
В уравнении неизвестно вычитаемое x+1/60.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
x+1/60=4/5-2/3
x+1/60=(4•3)/(5•3)-(2•5)/(3•5)
x+1/60=12/15-10/15
x+1/60=(12-10)/15
x+1/60=2/15
В уравнении неизвестно слагаемое x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
x=2/15-1/60
x=(2•4)/(15•4)-1/60
x=8/60-1/60
x=(8-1)/60
x=7/60
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









